Teorema sobre a fronteira de um conjunto
Um ponto \( x \) pertence à fronteira de um conjunto \( A \) quando toda vizinhança de \( x \) contém ao mesmo tempo pontos de \( A \) e do seu complementar \( X - A \). Essa é a ideia central: ao redor de \( x \) sempre encontramos elementos dos dois lados.
Isso significa que nenhuma vizinhança de \( x \) está totalmente dentro de \( A \) ou totalmente fora dele. O ponto fica justamente na transição entre o conjunto e o exterior.
Um exemplo para visualizar a definição
Para entender melhor, consideremos o intervalo aberto \( A = (0, 1) \) na reta real \( \mathbb{R} \). Esse é um caso simples e muito usado para ilustrar conceitos topológicos.
Os pontos 0 e 1 pertencem à fronteira de \( A \) porque, por menores que sejam as vizinhanças escolhidas, sempre surgem valores dentro do intervalo e valores fora dele.
- Ponto 1
Ao tomar uma vizinhança como \( (1 - \epsilon, 1 + \epsilon) \), com ε bem pequeno, percebemos que o lado esquerdo do intervalo está dentro de \( A \) e o lado direito está fora. O ponto 1 fica exatamente nesse limite, o que caracteriza um ponto de fronteira.
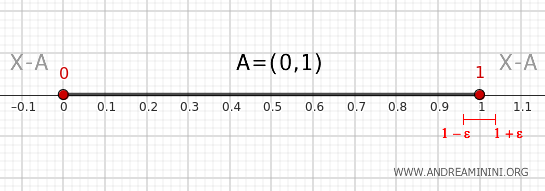
- Ponto 0
O mesmo raciocínio vale para o ponto 0. Uma vizinhança \( (0 - \epsilon, 0 + \epsilon) \) reúne valores pertencentes a \( A \) e valores que estão no complementar. Por isso, 0 também é um ponto de fronteira.
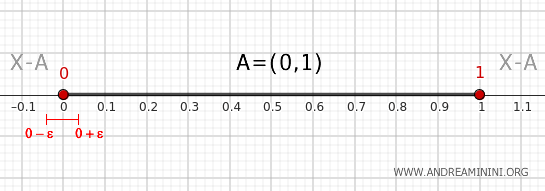
- Pontos dentro do intervalo
Já um ponto \( x \) estritamente entre 0 e 1 dispõe de vizinhanças totalmente contidas em \( A \). Nessas vizinhanças não aparecem elementos exteriores, portanto esses pontos não pertencem à fronteira.
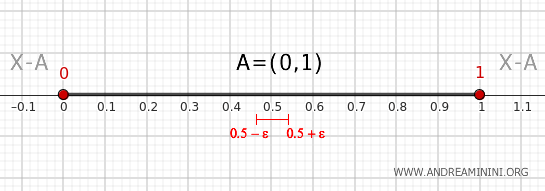
- Pontos fora do intervalo
Qualquer ponto fora de \( (0, 1) \), com exceção das extremidades, possui uma vizinhança completamente no complementar. Como essa vizinhança não toca \( A \), tais pontos não são de fronteira.
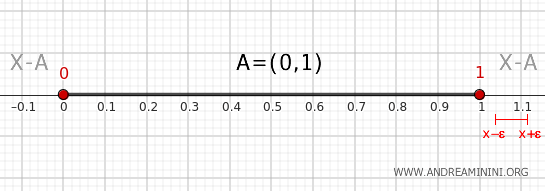
Assim, identificamos a fronteira do intervalo de forma precisa:
$$ \partial A = \{0,1\} $$
Essa caracterização é muito útil em topologia: para verificar se um ponto está na fronteira de um conjunto, basta observar se todas as suas vizinhanças atravessam tanto o interior quanto o exterior do conjunto.
A demonstração
A lógica do teorema pode ser entendida a partir de duas direções, que se complementam.
1] Suponha que \( x \in \partial A \)
Por definição, vale:
$$ x \in \text{Cl}(A) \quad \text{e} \quad x \notin \text{Int}(A) $$
Estar no fecho significa que toda vizinhança de \( x \) alcança \( A \). Não estar no interior significa que nenhuma vizinhança de \( x \) cabe inteiramente em \( A \). Logo, cada vizinhança também contém pontos do complementar. Isso confirma que toda vizinhança intersecta os dois conjuntos ao mesmo tempo.
2] Agora suponha que toda vizinhança de \( x \) intersecte \( A \) e também \( X - A \)
Nesse caso, \( x \) pertence ao fecho de \( A \) e ao fecho do complementar. Como o fecho do complementar é \( X - \text{Int}(A) \), segue que \( x \notin \text{Int}(A) \).
Assim, chegamos a:
$$ x \in \text{Cl}(A) \setminus \text{Int}(A) = \partial A $$
Isso completa a demonstração e confirma que o critério usado descreve exatamente os pontos de fronteira. O resultado é simples, elegante e extremamente útil em muitos contextos da topologia.