Convergência num espaço topológico

Em um espaço topológico $ X $, diz-se que um ponto $ x \in X $ é o limite de uma sequência $ (x_n) $ quando, para toda vizinhança $ U $ de $ x $, existe um número inteiro positivo $ N $ tal que, para todo $ n \geq N $, vale $ x_n \in U $.

De forma intuitiva, isso significa que a sequência $ (x_n) $ converge para $ x $ quando, a partir de certo ponto, todos os seus termos passam a permanecer dentro de qualquer região que contenha $ x $.

Essa ideia é expressa simbolicamente por:

$$ \lim_{n \to \infty} x_n = x $$

Nesse caso, dizemos que $ x $ é o limite da sequência $ (x_n) $.

Exemplo ilustrativo

Consideremos a sequência $ \left( \frac{1}{n} \right) $ no espaço topológico $ X = \mathbb{R} $, munido da topologia usual.

$$ x_n = \left( \frac{1}{n} \right) $$

Nosso objetivo é mostrar que essa sequência converge para 0, isto é, que 0 é o seu limite.

Seja $ U $ uma vizinhança arbitrária de 0.

Na topologia usual de $ \mathbb{R} $, toda vizinhança de 0 contém um intervalo aberto da forma $ (-\epsilon, \epsilon) $, com $ \epsilon > 0 $.

Precisamos então determinar um inteiro $ N \in \mathbb{N} $ tal que, para todo $ n \geq N $, tenhamos $ \frac{1}{n} \in (-\epsilon, \epsilon) $.

Dado $ \epsilon > 0 $, basta escolher $$ N = \left\lceil \frac{1}{\epsilon} \right\rceil. $$ Assim, para todo $ n \geq N $, vale:

$$ n \geq \frac{1}{\epsilon} \quad \Rightarrow \quad \frac{1}{n} \leq \epsilon $$

Consequentemente,

$$ \left| \frac{1}{n} \right| < \epsilon \quad \text{para todo } n \geq N. $$

Isso mostra que, para toda vizinhança $ U $ de 0, existe um índice $ N $ a partir do qual todos os termos da sequência pertencem a $ U $. Portanto,

$$ \lim_{n \to \infty} \frac{1}{n} = 0 $$

Concluímos, assim, que 0 é efetivamente o limite da sequência $ \left( \frac{1}{n} \right) $.

Em outras palavras, a sequência $ \frac{1}{n} $ converge para zero porque, a partir de certo índice, todos os seus termos permanecem dentro de qualquer vizinhança de zero.

A tabela a seguir apresenta, de forma ilustrativa, os dez primeiros termos da sequência:

$$ \begin{array}{|c|c|} \hline n & \frac{1}{n} \\ \hline 1 & 1 \\ 2 & 0.5 \\ 3 & 0.333 \\ 4 & 0.25 \\ 5 & 0.2 \\ 6 & 0.167 \\ 7 & 0.143 \\ 8 & 0.125 \\ 9 & 0.111 \\ 10 & 0.1 \\ \hline \end{array} $$

Por exemplo, se escolhermos $ N = 5 $, temos $ x_5 = \frac{1}{5} = 0.2 $. A partir desse ponto, todos os termos seguintes da sequência pertencem à vizinhança $ U = (0, 0.2) $.

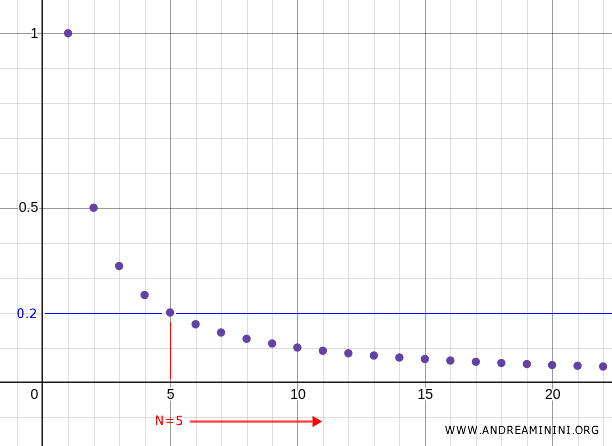
exemplo de ponto de convergência

O mesmo raciocínio vale para qualquer outra escolha de $ N $.

Por exemplo, se tomarmos $ N = 10 $, então $ x_{10} = 0.1 $, e, para todo $ n > 10 $, os termos da sequência pertencem à vizinhança $ U = (0, 0.1) $.

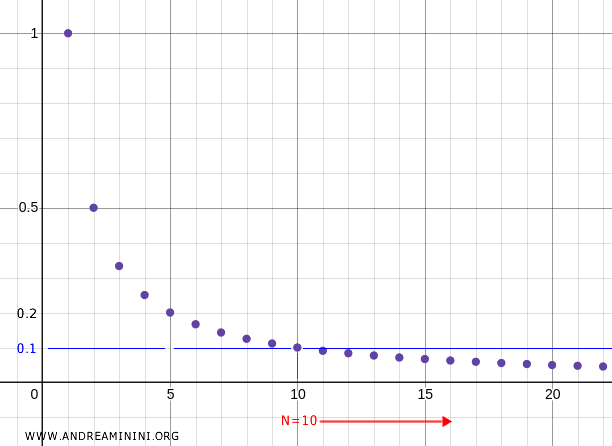
visualização da sucessão convergente

Concluímos, portanto, que 0 é o limite da sequência.

E assim sucessivamente.