Pontos de acumulação em topologia

Num espaço topológico $X$, dizemos que um ponto $x$ é um ponto de acumulação de um subconjunto $A \subseteq X$ quando toda vizinhança de $x$ intersecta $A$ em pelo menos um ponto distinto de $x$.

Intuitivamente, isso significa que é impossível isolar o ponto $x$ do conjunto $A$: por menor que seja a região considerada em torno de $x$, ela contém sempre algum ponto de $A$ diferente do próprio $x$.

De forma mais rigorosa, $x$ é um ponto de acumulação de $A$ se, para toda vizinhança $U$ de $x$, a interseção de $U$ com $A \setminus \{x\}$ é não vazia.

$$ U \cap (A \setminus \{x\}) \neq \emptyset $$

É importante notar que um ponto de acumulação não precisa pertencer ao conjunto $A$; ele pode perfeitamente estar fora do conjunto.

No espaço topológico real $\mathbb{R}$, munido da topologia usual, a ideia de ponto de acumulação é particularmente fácil de visualizar. Na reta real, um ponto $x$ é um ponto de acumulação de um subconjunto $A$ se toda vizinhança de $x$, isto é, qualquer intervalo aberto do tipo $(x-\epsilon, x+\epsilon)$, contém pelo menos um ponto de $A$ distinto de $x$.
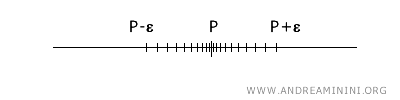
ilustração de um ponto de acumulação na reta real
A definição topológica permite generalizar esse conceito para o espaço $n$-dimensional $\mathbb{R}^n$. Nesse contexto mais geral, um ponto $x$ é um ponto de acumulação de um conjunto $A$ se toda vizinhança de $x$ possui uma interseção não vazia com $A$ em um ponto diferente do próprio $x$. Embora essa generalização seja menos intuitiva do ponto de vista geométrico, a ideia fundamental permanece a mesma.

Exemplos concretos
Observações

Exemplos concretos

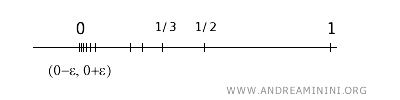
Consideremos o conjunto $A$ como um subconjunto de $\mathbb{R}$, munido da topologia usual.

$$ A = \left\{ \frac{1}{n} \mid n \in \mathbb{N}^+ \right\} $$

Esse conjunto é composto pelos pontos $ \frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \ldots $, isto é, $\{1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \ldots \}$.

Para verificar se $0$ é um ponto de acumulação de $A$, consideremos uma vizinhança aberta qualquer de $0$.

Toda vizinhança de $0$ contém um intervalo aberto $(a, b)$ tal que $a < 0 < b$.

Como $\frac{1}{n}$ converge para $0$ quando $n$ tende ao infinito, existe sempre algum valor de $\frac{1}{n}$ pertencente ao intervalo $(a, b)$, desde que $n$ seja suficientemente grande.

Assim, toda vizinhança de $0$ contém pelo menos um ponto de $A$ distinto de $0$.

Concluímos, portanto, que $0$ é um ponto de acumulação do conjunto $A$.

representação de um ponto de acumulação

Exemplo 2

Consideremos agora o conjunto $B$, também um subconjunto de $\mathbb{R}$ com a topologia usual.

$$ B = \left\{ n + \frac{1}{n} \mid n \in \mathbb{N}^+ \right\} $$

Esse conjunto contém os pontos $ 1 + 1, 2 + \frac{1}{2}, 3 + \frac{1}{3}, \ldots $, isto é, $\{2, 2.5, 3.333\ldots, \ldots \}$.

Analisemos o ponto $1$.

Toda vizinhança aberta de $1$ contém necessariamente um intervalo $(a, b)$ com $a < 1 < b$.

No entanto, todos os elementos de $B$ são estritamente maiores que $1$. Portanto, existe uma vizinhança de $1$ suficientemente pequena que não contém nenhum ponto de $B$.

Conclui-se, assim, que $1$ não é um ponto de acumulação de $B$.

Exemplo 3

Consideremos agora o conjunto $(0, 1]$ como um subconjunto de $\mathbb{R}$, munido da topologia usual.

Queremos identificar quais são os seus pontos de acumulação.

De acordo com a definição, um ponto $x$ é um ponto de acumulação de $(0, 1]$ se toda vizinhança de $x$ intersecta $(0, 1]$ em pelo menos um ponto distinto de $x$.

Pontos interiores de $(0,1]$
Seja $x \in (0, 1]$. Em torno de qualquer desses pontos existem sempre outros pontos do intervalo $(0, 1)$ arbitrariamente próximos. Por isso, toda vizinhança de $x$ intersecta $(0, 1]$ em pontos distintos de $x$. Logo, todo ponto de $(0, 1]$ é um ponto de acumulação desse conjunto.
Pontos de fronteira de $(0,1]$
Consideremos agora as extremidades do intervalo.
- Ponto $0$ : Embora $0$ não pertença a $(0, 1]$, toda vizinhança de $0$ contém pontos positivos arbitrariamente próximos de $0$, que pertencem ao intervalo. Assim, $0$ é um ponto de acumulação de $(0, 1]$.

- Ponto $1$ : Como $1$ pertence a $(0, 1]$, toda vizinhança de $1$ contém pontos de $(0, 1)$ diferentes de $1$. Portanto, $1$ também é um ponto de acumulação de $(0, 1]$.
Pontos exteriores a $[0, 1]$
Para completar a análise, consideremos um ponto $x \notin [0, 1]$. Se $x < 0$ ou $x > 1$, é sempre possível encontrar uma vizinhança aberta de $x$ completamente disjunta de $(0, 1]$.
Por exemplo, se $x < 0$, pode-se escolher um intervalo aberto $(x - \epsilon, x + \epsilon)$ com $\epsilon$ suficientemente pequeno para que ele não contenha nenhum ponto de $(0, 1]$. De modo análogo, se $x > 1$, existe um intervalo aberto centrado em $x$ inteiramente disjunto de $(0, 1]$. Assim, nenhum ponto exterior ao intervalo fechado $[0, 1]$ é ponto de acumulação de $(0, 1]$.

Em conclusão, os pontos de acumulação de $(0, 1]$, no espaço topológico $\mathbb{R}$ munido da topologia usual, são exatamente os elementos do intervalo fechado $[0, 1]$.

Exemplo 4

Vamos agora determinar o conjunto dos pontos de acumulação de $ A = (0, 1] $ quando $ \mathbb{R} $ é considerado com a topologia do limite inferior.

A topologia do limite inferior sobre $ \mathbb{R} $, também conhecida como topologia de Sorgenfrey, é definida a partir de uma base formada por intervalos do tipo $[a, b)$, com $ a < b $. Os conjuntos abertos dessa topologia são obtidos como uniões arbitrárias desses intervalos básicos.

Recordemos que um ponto $x$ é um ponto de acumulação de um conjunto $A$ quando toda vizinhança de $x$ contém pelo menos um ponto de $A$ diferente do próprio $x$.

Com isso em mente, analisemos os diferentes casos possíveis.

Para $x \in (0, 1)$
Qualquer vizinhança de $x$ nessa topologia contém um intervalo básico da forma $[x, x + \epsilon)$, que inclui infinitos pontos pertencentes a $A$. Assim, todo ponto de $(0, 1)$ é um ponto de acumulação de $A$.
Para $x = 1$
As vizinhanças de $1$ na topologia do limite inferior são intervalos do tipo $[1, 1 + \epsilon)$. Cada uma delas contém pontos de $A$ distintos de $1$, pois inclui valores do intervalo $(0, 1)$ arbitrariamente próximos de $1$ pela esquerda. Logo, $1$ também é um ponto de acumulação de $A$.
Para $x = 0$
Toda vizinhança de $0$ é da forma $[0, 0 + \epsilon)$ e intersecta o conjunto $A$ em infinitos pontos de $(0, 1]$. Portanto, $0$ é igualmente um ponto de acumulação de $A$.
Para $x < 0$ ou $x > 1$
Nesses casos, é possível escolher uma vizinhança básica $[x, x + \epsilon)$ que seja completamente disjunta de $A$. Assim, tais pontos não são pontos de acumulação.

Concluímos, portanto, que os pontos de acumulação do conjunto $ A = (0, 1] $, na topologia do limite inferior sobre $ \mathbb{R} $, coincidem exatamente com os elementos do intervalo fechado $[0, 1]$.

Em outras palavras, o conjunto de todos os pontos de acumulação de $ A $ é $[0, 1]$.

Observações

Encerramos com algumas observações que ajudam a contextualizar o papel dos pontos de acumulação em topologia.

A aderência de um conjunto
A aderência de um subconjunto $A$ de um espaço topológico $X$ é definida como $$ \text{Cl}(A) = A \cup A' $$ onde $A'$ representa o conjunto dos pontos de acumulação de $A$. Em termos conceituais, a aderência é o menor conjunto fechado que contém $A$.
Convergência e pontos de acumulação
Se $ A \subseteq \mathbb{R} $ é considerado com a topologia usual e $ x $ é um ponto de acumulação de $ A $, então existe uma sequência $ \{x_i\} \subseteq A \setminus \{x\} $ que converge para $ x $. Note-se que o ponto de acumulação pode não pertencer ao conjunto $ A $.
Unicidade do limite
Na topologia usual de $ \mathbb{R} $, o limite de uma sequência, quando existe, é único. Essa propriedade, no entanto, não é válida em todas as topologias. Em espaços que não satisfazem o axioma de Hausdorff, uma mesma sequência pode convergir para mais de um ponto distinto.

Essas observações destacam a importância dos pontos de acumulação como ferramenta central para compreender a estrutura topológica dos conjuntos e o comportamento dos processos de convergência.