Subespaço Topológico

Um subespaço topológico é um subconjunto de um espaço topológico que herda, de forma natural, a topologia do espaço original.

Seja $ (X, T) $ um espaço topológico, onde $ X $ é um conjunto e $ T $ é a família de conjuntos abertos que define a topologia em $ X $. Seja $ Y \subseteq X $. A topologia de subespaço em $ Y $ é definida por: \[ T_Y = \{ U \cap Y \mid U \in T \} \]

Em outras palavras, um conjunto $ V \subseteq Y $ é aberto na topologia de subespaço se, e somente se, puder ser escrito como a interseção de $ Y $ com um conjunto aberto $ U $ do espaço original $ X $.

Assim, todos os conjuntos abertos na topologia de subespaço de $ Y $ são da forma $ U \cap Y $, com $ U $ aberto em $ X $.

$$ V_{aberto \ em \ Y} = U \cap Y $$

De maneira análoga, todos os conjuntos fechados na topologia de subespaço de $ Y $ têm a forma $ C \cap Y $, onde $ C $ é fechado em $ X $.

$$ V_{fechado \ em \ Y} = C \cap Y $$

Observação. Conjuntos abertos na topologia de subespaço $ Y $ nem sempre são abertos no espaço $ X $. Pode acontecer de um conjunto ser aberto em $ Y $ e fechado em $ X $, ou o contrário. Alguns conjuntos podem ser abertos e fechados em ambos. Além disso, há conjuntos chamados "clopen", que são simultaneamente abertos e fechados. Um exemplo desse tipo é discutido na primeira seção destas notas.

Exemplo
Propriedades da topologia de subespaço
Observações

Exemplo

Considere o espaço topológico $ \mathbb{R} $ com a topologia padrão, na qual os conjuntos abertos são intervalos abertos.

Seja $ Y = [0, 1] $ um subconjunto de $ \mathbb{R} $.

A topologia de subespaço em $ Y $ é formada por todos os conjuntos da forma:

$$ U \cap [0, 1] $$

em que $ U $ é um conjunto aberto em $ \mathbb{R} $.

Por exemplo, o conjunto (-1, 0.5) é aberto no espaço $ \mathbb{R} $.

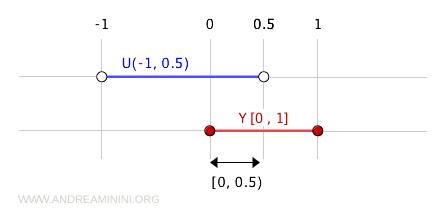
Exemplo de um subespaço topológico

A interseção de (-1, 0.5) com $ Y = [0, 1] $ é um conjunto aberto na topologia de subespaço de $ Y $:

$$ (-1, 0.5) \cap [0, 1] = [0, 0.5) $$

O intervalo $ [0, 0.5) $ é, portanto, aberto no subespaço $ Y $.

Já o intervalo $ [0, 0.5] $ é fechado na topologia de subespaço de $ Y $, pois pode ser obtido como a interseção do conjunto fechado [-1, 0.5] em $ X $ com $ Y $:

$$ [-1, 0.5] \cap [0, 1] = [0, 0.5] $$

Em resumo, o subespaço $ Y $ herda de $ X $ uma topologia na qual os conjuntos abertos em $ Y $ são exatamente as interseções de $ Y $ com os conjuntos abertos de $ X $.

Observação. Conjuntos como [0,a) ou (a,1], com 0<a<1, não são abertos na topologia padrão de $ \mathbb{R} $, mas são abertos na topologia de subespaço. Isso ocorre porque podem ser expressos como interseções de $ Y = [0,1] $ com conjuntos abertos de $ \mathbb{R} $. Por exemplo: $$ (-1,0.5) \cap [0,1] = [0,0.5) $$ Assim, o intervalo [0,0.5) é aberto no subespaço $ Y $, embora não o seja na topologia padrão de $ \mathbb{R} $.

Há também conjuntos que são abertos tanto em $ Y $ quanto em $ X $, como (0.2, 0.8), e conjuntos que são fechados em ambos, como [0.2, 0.8].

Na topologia de subespaço $ Y = [0, 1] $, o conjunto $ [0, 1] $ é simultaneamente aberto e fechado.

Abertura
Para mostrar que $ [0, 1] $ é aberto no subespaço $ Y $, basta encontrar um conjunto aberto $ U $ em $ \mathbb{R} $ tal que $ U \cap Y = [0, 1] $. Escolhendo $ U = \mathbb{R} $, que é aberto em $ \mathbb{R} $, obtemos: $$ U \cap Y = \mathbb{R} \cap [0, 1] = [0, 1] $$ Assim, $ [0, 1] $ é aberto em $ Y $.
Fechamento
Para provar que $ [0, 1] $ é fechado no subespaço $ Y $, procuramos um conjunto fechado $ C $ em $ \mathbb{R} $ tal que $ C \cap Y = [0, 1] $. Se tomarmos $ C = [0, 1] $, que é fechado em $ \mathbb{R} $, teremos: $$ C \cap Y = [0, 1] \cap [0, 1] = [0, 1] $$ Portanto, $ [0, 1] $ é fechado em $ Y $.
Observação: Outra forma de verificar o fechamento é considerar o complemento de $ [0, 1] $ em $ Y $, que é o conjunto vazio. Como o conjunto vazio é aberto em qualquer topologia, e o complemento de um conjunto aberto é fechado, segue-se que $ [0, 1] $ é fechado em $ Y $.

Consequentemente, em $ Y = [0, 1] $, o conjunto $ [0, 1] $ é simultaneamente aberto e fechado. Conjuntos desse tipo são chamados de "clopen", uma junção das palavras inglesas "closed" e "open".

Exemplo 2

Consideremos a topologia padrão sobre o conjunto dos números reais $ \mathbb{R} $.

Nessa topologia, todo intervalo (a,b) com a < b é aberto.

Um exemplo típico de subespaço topológico de $ \mathbb{R} $ é o conjunto dos números inteiros $ \mathbb{Z} $, já que cada inteiro pode ser obtido como a interseção de intervalos abertos em $ \mathbb{R} $.

Por exemplo, o número inteiro 7 pode ser obtido como a interseção do conjunto aberto (6.5,7.5) em $ \mathbb{R} $ com o conjunto $ \mathbb{Z} $:

$$ (6.5,7.5) \cap \mathbb{Z} = \{ 7 \} $$

De modo análogo, qualquer outro número inteiro pode ser obtido da mesma forma. Assim, cada elemento de $ \mathbb{Z} $ é aberto na topologia de subespaço de $ \mathbb{Z} $.

Portanto, toda parte de $ \mathbb{Z} $ é aberta nessa topologia de subespaço.

Por exemplo, para o conjunto aberto (5.5,8.5):

$$ (5.5,8.5) \cap \mathbb{Z} = \{ 6, 7, 8 \} $$

Esse subespaço topológico em $ \mathbb{Z} $ é conhecido como topologia discreta.

Observação: A topologia discreta em $ \mathbb{Z} $ não é, por si só, um subespaço da topologia padrão de $ \mathbb{R} $, mas uma topologia independente. No entanto, a topologia herdada de $ \mathbb{R} $ por $ \mathbb{Z} $ é equivalente à topologia discreta em $ \mathbb{Z} $.

Exemplo 3

Consideremos o espaço euclidiano tridimensional $ \mathbb{R}^3 $, munido da topologia padrão, na qual os conjuntos abertos são definidos como uniões de bolas abertas.

Tomemos a superfície da esfera unitária $ S^2 $, definida como o conjunto de todos os pontos de $ \mathbb{R}^3 $ cuja distância à origem é igual a 1:

$$ S^2 = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1 \} $$

A topologia de subespaço em $ S^2 $ é então dada por:

$$ T_{S^2} = \{ U \cap S^2 \mid U \text{ é aberto em } \mathbb{R}^3 \} $$

Em outras palavras, um conjunto $ V \subseteq S^2 $ é aberto na topologia de subespaço se, e somente se, puder ser descrito como a interseção de $ S^2 $ com algum conjunto aberto $ U $ de $ \mathbb{R}^3 $.

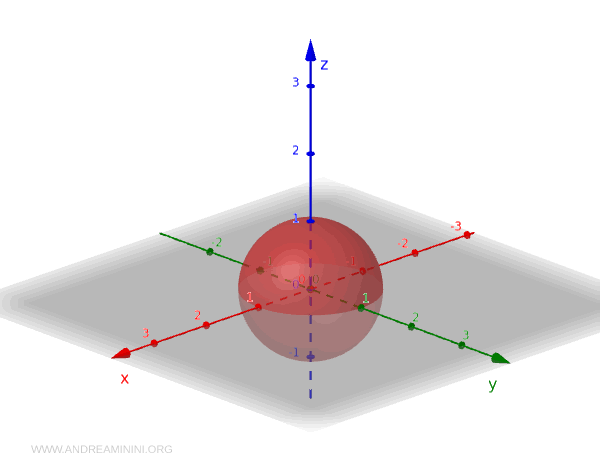
Superfície esférica como subespaço de R3

Vejamos alguns exemplos de conjuntos abertos em $ S^2 $:

União de conjuntos abertos em $ \mathbb{R}^3 $
Considere o conjunto aberto $ U = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 < 2 \} $.
Sua interseção com $ S^2 $ é: $$ U \cap S^2 = S^2 $$ pois, para todos os pontos de $ S^2 $, temos $ x^2 + y^2 + z^2 = 1 < 2 $. Logo, $ S^2 $ é aberto na sua própria topologia de subespaço.
Uma parte da superfície esférica
Consideremos agora o conjunto $ U = \{ (x, y, z) \in \mathbb{R}^3 \mid z > 0 \} $.
Sua interseção com $ S^2 $ é $$ U \cap S^2 = \{ (x, y, z) \in S^2 \mid z > 0 \} $$.
Esse conjunto corresponde à semiesfera superior e é aberto na topologia de subespaço $ T_{S^2} $.
Estabilidade dos conjuntos abertos
Tanto o conjunto vazio $ \emptyset $ quanto $ S^2 $ são abertos em $ S^2 $.
- A interseção de um número finito de conjuntos abertos em $ S^2 $ é novamente aberta em $ S^2 $.
- A união arbitrária de conjuntos abertos em $ S^2 $ também é aberta em $ S^2 $.

Em síntese, a superfície esférica $ S^2 $, considerada como subespaço de $ \mathbb{R}^3 $, herda naturalmente a topologia padrão do espaço euclidiano. Os conjuntos abertos em $ S^2 $ são precisamente as interseções de $ S^2 $ com conjuntos abertos de $ \mathbb{R}^3 $.

Propriedades da topologia de subespaço

A topologia de subespaço apresenta as seguintes propriedades fundamentais:

Conjuntos abertos
Todos os conjuntos abertos em $ Y $ têm a forma $ U \cap Y $, onde $ U $ é aberto em $ X $.
Conjunto vazio e conjunto total
Tanto o conjunto vazio $ \emptyset $ quanto $ Y $ são sempre abertos em $ Y $:
- $ \emptyset $ é aberto porque $ \emptyset = \emptyset \cap Y $.
- $ Y $ é aberto porque $ Y = X \cap Y $.
Interseções finitas
A interseção de um número finito de conjuntos abertos em $ Y $ é novamente aberta em $ Y $. Se $ V_1, \ldots, V_n $ são abertos em $ Y $, então: $$ V_1 \cap \cdots \cap V_n = (U_1 \cap Y) \cap \cdots \cap (U_n \cap Y) = (U_1 \cap \cdots \cap U_n) \cap Y $$ com cada $ U_i $ aberto em $ X $. Como a interseção finita de conjuntos abertos em $ X $ é aberta, o resultado também é aberto em $ Y $.
Uniões arbitrárias
A união arbitrária de conjuntos abertos em $ Y $ também é aberta em $ Y $. Se, para cada $ \alpha $ de um conjunto de índices $ I $, $ V_\alpha $ é aberto em $ Y $, então: $$ \bigcup_{\alpha \in I} V_\alpha = \bigcup_{\alpha \in I} (U_\alpha \cap Y) = \left( \bigcup_{\alpha \in I} U_\alpha \right) \cap Y $$ Como a união de conjuntos abertos em $ X $ é aberta, o mesmo vale para $ Y $.

Observações

Alguns comentários adicionais sobre subespaços topológicos:

A topologia padrão de um subespaço $ Y \subseteq \mathbb{R}^n $ coincide exatamente com a topologia de subespaço herdada de $ \mathbb{R}^n $.
Exemplo. Considere o conjunto $ Y = [-1,0) \cup (0,1] $, um subconjunto de $ \mathbb{R} $. Na topologia padrão de $ Y $, os intervalos [-1,0) e (0,1] são abertos, pois podem ser obtidos como interseções de $ Y $ com conjuntos abertos de $ \mathbb{R} $. Por exemplo, para os conjuntos abertos (-1.5,0.5) e (0,1.5) em $ \mathbb{R} $: $$ (-1.5,0.5) \cap Y = [-1,0) $$ $$ (0,1.5) \cap Y = (0,1] $$ Assim, a topologia padrão em $ Y $ é equivalente à topologia de subespaço herdada da topologia padrão de $ \mathbb{R} $. Nesse caso, os intervalos [-1,0) e (0,1] também são fechados em $ Y $, pois o complemento de [-1,0) é (0,1] e vice-versa. Dessa forma, ambos são conjuntos simultaneamente abertos e fechados ("clopen") na topologia padrão de $ Y $.
Teorema da base da topologia de subespaço
Esse teorema estabelece que, se $ B_X $ é uma base da topologia de um espaço topológico $ X $ e $ Y \subset X $, então o conjunto de todas as interseções $ B \cap Y $ forma uma base $ B_Y $ da topologia de subespaço em $ Y $: $$ B_Y = \{ B \cap Y \mid B \in B_X \} $$

E assim por diante.