Bola Aberta

Em topologia, uma bola aberta, também chamada de vizinhança circular, disco ou esfera aberta, é o conjunto formado por todos os pontos cuja distância até um ponto fixo, o centro $ c $, é menor que um certo valor positivo, o raio $ r $. Podemos escrever essa ideia da seguinte forma: $$ B(c, r) = \{ x \in M \mid d(c, x) < r \} $$

Esse conceito surge no contexto de um espaço métrico ($ M $), onde $ d $ é uma métrica, isto é, uma função que mede a distância entre quaisquer dois pontos do espaço.

Assim, para definir completamente uma bola aberta, basta conhecer o seu centro e o seu raio.

O termo "aberta" tem um significado específico em topologia: cada ponto situado dentro da bola pode servir de centro para outra bola ainda menor, inteiramente contida na original. Essa propriedade caracteriza o comportamento dos conjuntos abertos nos espaços métricos.

Nota: As bolas abertas são invariantes por translação e por escala. Isso significa que deslocá-las ou alterar o seu tamanho não modifica a sua natureza matemática.

Para visualizar melhor, consideremos o plano $ \mathbb{R}^2 $. A distância entre um ponto $ p = (x, y) $ e o centro $ c = (x_0, y_0) $ é dada pela métrica euclidiana, amplamente conhecida da geometria clássica:

$$ d(p,c) = \sqrt{(x-x_0)^2+(y-y_0)^2} $$

As bolas abertas têm um papel central na construção da estrutura topológica dos espaços métricos. No caso do plano, elas formam a base da topologia padrão de $ \mathbb{R}^2 $, que é a topologia normalmente utilizada em análise e geometria.

Em termos formais, essa topologia é descrita pelo conjunto:

$$ B = \{ B(p, r) \ | \ p \in \mathbb{R}^2, \ r > 0 \} $$

Aqui, $ p $ representa um ponto genérico $ (x,y) $ do plano e $ r $ indica o raio da bola correspondente.

a topologia padrão em R^2

Embora seja possível definir muitas outras topologias sobre $ \mathbb{R}^2 $, a topologia induzida pelas bolas abertas euclidianas é a mais utilizada por ser intuitiva, bem comportada e compatível com os métodos da análise matemática.

Dentro de uma bola aberta, cada ponto $ q \in B(p,r) $ pode ser o centro de uma nova bola $ B(q, \epsilon) $, menor e totalmente contida na primeira. Essa característica está no coração do conceito topológico de abertura.

De forma precisa, essa propriedade é expressa por:

$$ \forall \ q \in B(p,r) \ \exists \ \epsilon > 0 \ \text{tal que} \ B(q,\epsilon) \subset B(p,r) $$

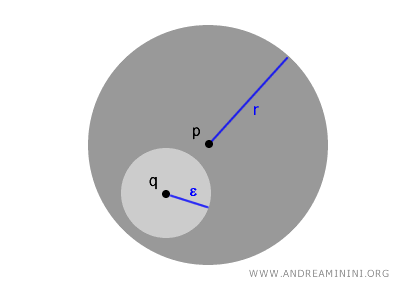
exemplo de uma bola aberta

Esse processo pode se repetir indefinidamente, revelando como as bolas abertas estruturam e organizam o comportamento dos conjuntos num espaço topológico.