Espaço Topológico Normal

Um espaço topológico $ X $ é chamado normal quando satisfaz duas condições fundamentais:

Todo conjunto unitário é fechado
Em qualquer ponto $ x \in X $, o conjunto $\{x\}$ deve ser fechado na topologia considerada.
Conjuntos fechados e disjuntos podem ser separados por abertos disjuntos
Se $ A $ e $ B $ são fechados e não compartilham elementos, ou seja, $ A \cap B = \emptyset $, então existem abertos $ U $ e $ V $ tais que:
- $ A \subset U $
- $ B \subset V $
- $ U \cap V = \emptyset $, garantindo a separação.

A noção de normalidade é importante porque permite isolar conjuntos fechados que não se intersectam. Em um espaço normal, sempre é possível envolver cada conjunto com um aberto adequado, evitando qualquer sobreposição.

Esse tipo de separação desempenha um papel essencial na construção de funções contínuas capazes de distinguir pontos ou regiões do espaço, o que torna os espaços normais especialmente relevantes em diversos contextos da topologia.

Exemplo Prático
Notas Adicionais

Exemplo Prático

Considere o espaço $ X = \mathbb{R} $, munido da topologia padrão formada por intervalos abertos $ (a, b) $. Vamos analisar dois conjuntos fechados e disjuntos:

$ A = \{0\} $, composto por um único ponto.
$ B = [2, 3] $, um intervalo fechado.

Ambos são fechados na topologia usual e não compartilham elementos, portanto são disjuntos.

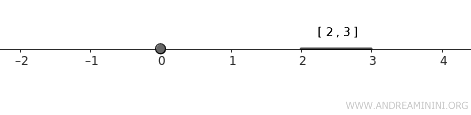
exemplo

Nota. O conjunto $ A $ é fechado por ser formado apenas por um ponto isolado. Já o conjunto $ B $, sendo um intervalo fechado, também é fechado na topologia padrão.

Para separar esses dois conjuntos, basta encontrar abertos disjuntos que os envolvam. Podemos escolher $ U = (-1, 1) $, que contém $ A = \{0\} $.

$$ A \subset U = (-1,1) $$

Para $ B = [2,3] $, um aberto possível é $ V = (1, 4) $, que o contém inteiramente.

$$ B \subset V = (1,4) $$

Os abertos $ U $ e $ V $ são disjuntos porque $ U \cap V = \emptyset $. Isso confirma que a reta real, com a topologia padrão, é um exemplo de espaço normal.

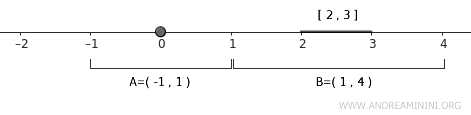
exemplo

O mesmo raciocínio se aplica a qualquer outro par de fechados disjuntos: sempre será possível encontrar abertos separados que os contenham, sem qualquer ponto em comum.

Notas Adicionais

Algumas observações importantes para aprofundar o tema:

A reta real $ \mathbb{R} $ com a topologia usual é um espaço normal
Além de cumprir a condição de regularidade, que permite separar pontos de fechados usando abertos distintos, também satisfaz a forma mais forte de separação definida pela normalidade.
Todo espaço métrico é normal
Espaços munidos de uma métrica são sempre normais, pois a própria noção de distância permite separar conjuntos fechados de maneira controlada.
Todo espaço normal é regular
A normalidade implica regularidade, o que torna essa propriedade mais forte dentro da hierarquia das condições de separação.

Essas ideias ajudam a compreender por que os espaços normais ocupam um papel central na topologia e em muitas construções matemáticas baseadas em continuidade e separação.