Interior de um Conjunto

Em um espaço topológico \( X \), o interior de um conjunto \( A \) é a união de todos os subconjuntos abertos contidos em \( A \). Costuma ser indicado por \( \text{Int}(A) \) ou \( A^\circ \).

O interior de um conjunto é o maior conjunto aberto contido integralmente em \( A \).

Não existe nenhum subconjunto aberto de \( A \) que seja maior do que o seu interior.

Nota: O interior de um conjunto é, por definição, uma união de conjuntos abertos, portanto é sempre um conjunto aberto.

De forma rigorosa, o interior de \( A \) é o conjunto de todos os pontos de \( A \) que possuem uma vizinhança aberta inteiramente contida em \( A \).

$$ \text{Int}(A) = \bigcup \{ U \subseteq A : U \text{ é aberto em } X \} $$

Em outras palavras, um ponto \( x \) pertence ao interior de \( A \) se existe um conjunto aberto \( U \) tal que \( x \in U \) e \( U \subseteq A \).

É importante lembrar que o interior de um conjunto \( A \) depende da topologia do espaço \( X \) em que ele está definido, e não apenas do conjunto \( A \). Assim, o interior pode variar conforme a topologia escolhida.

Exemplo Prático

Consideremos o conjunto \( A = [0,1] \) em \( \mathbb{R} \) com a topologia padrão.

Esse intervalo contém todos os números reais entre 0 e 1, incluindo os extremos.

Nesse caso, o interior de \( A \) é \( (0,1) \).

$$ \text{Int}(A) = (0,1) $$

Esse é o maior intervalo aberto contido em \( A \), excluindo os pontos 0 e 1, pois nenhum deles pertence a um subconjunto aberto inteiramente contido em \( A \).

Exemplo 2

Agora consideremos o conjunto \( A = [0,1) \) em \( \mathbb{R} \), ainda com a topologia padrão.

Esse conjunto contém todos os números reais de 0 até 1, incluindo 0 e excluindo 1, formando um intervalo fechado à esquerda e aberto à direita.

O interior de \( A \) permanece o mesmo do exemplo anterior:

\[ \text{Int}(A) = (0,1) \]

Isso acontece porque o interior é a união de todos os subconjuntos abertos inteiramente contidos em \( A \). O maior deles continua sendo \( (0,1) \).

Nota: Em \( \mathbb{R} \) com a topologia padrão, os conjuntos abertos são uniões de intervalos abertos. Assim, em \( [0,1) \), o maior subconjunto aberto contido é \( (0,1) \), pois 0 não pertence a nenhum intervalo aberto inteiramente incluído em \( A \).

Exemplo 3

Agora consideremos o conjunto \( A = [0,1) \) em uma topologia discreta sobre \( X \).

Em um espaço com topologia discreta, todos os subconjuntos são abertos.

Isso significa que qualquer ponto de \( A \) possui uma vizinhança aberta totalmente contida em \( A \).

Na topologia discreta sobre \( \mathbb{R} \), qualquer subconjunto é aberto, seja um intervalo, um conjunto finito ou combinações arbitrárias de pontos. Assim, em \( A = [0,1) \), conjuntos como \( (0,0.5) \), \( (0.25,0.75) \), \( (0,1) \) e também \( [0,0.25] \), além do conjunto vazio e do próprio \( [0,1) \), são todos abertos.

Nessa topologia, o próprio conjunto \( A \) é aberto.

Portanto, o interior de \( A \) coincide com o próprio conjunto:

$$ \text{Int}(A) = A = [0,1) $$

Em uma topologia discreta, o interior de qualquer conjunto coincide sempre com o conjunto original.

Nota: Este exemplo destaca como a escolha da topologia altera a estrutura das vizinhanças e do interior. O interior depende da topologia do espaço \( X \), e não apenas do conjunto \( A \).

Exemplo 4

Consideremos agora um espaço topológico \( X \) formado pelos pontos \( \{a, b, c\} \), com uma topologia discreta.

Nesse espaço, qualquer subconjunto é aberto:

• Por definição, \( \emptyset \) e \( \{a, b, c\} \) são abertos.
• Os conjuntos unitários \( \{a\} \), \( \{b\} \) e \( \{c\} \) também são abertos, pois na topologia discreta cada ponto é aberto.
• Os subconjuntos com dois elementos, como \( \{a, b\} \), \( \{a, c\} \) e \( \{b, c\} \), também são abertos.

Consideremos o conjunto \( A = \{b, c\} \) em \( X \):

Por definição, o interior de \( A \) é a união de todos os subconjuntos abertos contidos em \( A \).

Nesse caso, os subconjuntos abertos de \( A \) são \( \{b\} \), \( \{c\} \) e \( \{b, c\} \).

\[ \text{Int}(A) = \{b\} \cup \{c\} \cup \{b, c\} = \{b, c\} \]

Portanto, o interior de \( A \) coincide com o próprio conjunto.

Concluímos que \( \text{Int}(A) = A \).

Nota: Esse resultado vale para qualquer subconjunto \( S \subseteq X \) em uma topologia discreta. Como todos os subconjuntos são abertos, sempre temos \( \text{Int}(S) = S \).

Teorema do Interior de um Conjunto

Em um espaço topológico \( X \), dado um subconjunto \( S \) e um elemento \( y \in X \), o ponto \( y \) pertence ao interior de \( S \), indicado por \( \operatorname{Int}(S) \), se e somente se existe um conjunto aberto \( U \) tal que \( y \in U \subseteq S \). Em notação matemática, $$ y \in \text{Int}(S) \iff \exists \ U \text{ aberto, com } y \in U \subseteq S $$

Em outras palavras, um ponto \( y \) está no interior de \( S \) se existe uma vizinhança aberta \( U \) que o contenha e que esteja inteiramente incluída em \( S \).

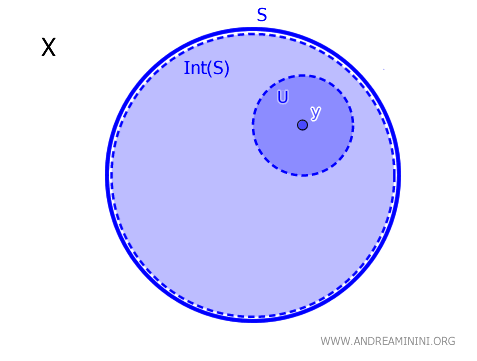
Esse teorema fornece um critério necessário e suficiente para determinar se um ponto \( y \) pertence ao interior de um conjunto \( S \) em um espaço topológico \( X \).

Demonstração

• Condição necessária: Se \( y \) pertence ao interior de \( S \), por definição existe um conjunto aberto \( U \) em \( X \) tal que \( y \in U \) e \( U \subseteq S \). Assim, se \( y \in \operatorname{Int}(S) \), necessariamente existe um conjunto aberto contendo \( y \) e incluído em \( S \).
• Condição suficiente: Se existe um conjunto aberto \( U \) tal que \( y \in U \subseteq S \), então, pela definição de interior, todos os pontos de \( U \) pertencem a \( \operatorname{Int}(S) \). Logo, \( y \in \operatorname{Int}(S) \).

Nota: Este teorema é fundamental, pois estabelece um vínculo direto entre conjuntos abertos e interior. Ele desempenha um papel central no estudo da continuidade e de diversas propriedades topológicas.

Exemplo

Consideremos o conjunto \( A = [1,3] \) de números reais, isto é, o intervalo fechado de 1 a 3 no espaço topológico \( \mathbb{R} \) com a topologia padrão.

$$ A = [1,3] $$

Esse conjunto contém todos os pontos entre 1 e 3, incluindo os extremos.

Para determinar o seu interior, aplicaremos o teorema do interior de um conjunto.

Determinação do Interior de \( A \)

Buscamos um conjunto aberto \( U \) tal que \( U \subseteq A \) e todos os seus pontos pertençam a \( \operatorname{Int}(A) \).

1. Escolha de \( U \)
   Tomemos \( U = (1,3) \), o intervalo aberto entre 1 e 3. Esse conjunto é aberto na topologia padrão de \( \mathbb{R} \) porque intervalos abertos são abertos nesse espaço.
2. Verificação de que \( U \subseteq A \)
   Observa-se que todos os pontos de \( U = (1,3) \) pertencem a \( A = [1,3] \), com exceção dos extremos \( 1 \) e \( 3 \), que não estão em \( U \) porque intervalos abertos não incluem os seus extremos.

Assim, \( U \) é um conjunto aberto inteiramente contido em \( A \), o que garante que todos os seus pontos pertençam ao interior de \( A \). Em consequência, o interior de \( A \), \( \operatorname{Int}(A) \), é exatamente \( (1,3) \).

Nota: O interior de \( A \) é o intervalo aberto \( (1,3) \). Os extremos \( 1 \) e \( 3 \) não pertencem a \( \operatorname{Int}(A) \) porque não existe conjunto aberto contido em \( A \) que os inclua.

Propriedades do Interior

Apresentam-se a seguir propriedades fundamentais do interior de conjuntos em espaços topológicos. Cada uma delas evidencia relações importantes entre interior, fecho, união e interseção, algumas das quais podem, à primeira vista, parecer contraintuitivas.

• Propriedade da União dos Interiores
  A união dos interiores de dois conjuntos está sempre contida no interior da sua união. No entanto, essa inclusão não implica necessariamente igualdade. $$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
• Propriedade da Interseção dos Interiores
  A interseção dos interiores de dois conjuntos coincide exatamente com o interior da sua interseção. $$ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) $$
• Relação entre o Interior do Complemento e o Complemento do Fecho
  O interior do complemento de um conjunto \( A \) é igual ao complemento do seu fecho. $$ \text{Int}(X - A) = X - \text{Cl}(A) $$
• Relação entre o Fecho do Complemento e o Complemento do Interior
  O fecho do complemento de um conjunto \( A \) coincide com o complemento do seu interior. $$ \text{Cl}(X - A) = X - \text{Int}(A) $$

Notas

Apresentam-se agora algumas observações que complementam as propriedades do interior.

• Se \( U \) é aberto em \( X \) e \( U \subseteq A \), então \( U \subseteq \operatorname{Int}(A) \)
  Se \( U \) é um conjunto aberto em \( X \) e está contido em \( A \), então \( U \) também está contido no interior de \( A \). Como \( \operatorname{Int}(A) \) é o maior conjunto aberto contido em \( A \), qualquer aberto \( U \subseteq A \) deve necessariamente estar incluído em \( \operatorname{Int}(A) \).
• Se \( A \subseteq B \), então \( \operatorname{Int}(A) \subseteq \operatorname{Int}(B) \)
  Se um conjunto \( A \) está contido em um conjunto \( B \), então o interior de \( A \) está contido no interior de \( B \). Isso ocorre porque qualquer conjunto aberto contido em \( A \) também é subconjunto de \( B \). Assim, a operação de interior preserva a inclusão.
• Um conjunto \( A \) é aberto se e somente se \( A = \operatorname{Int}(A) \)
  Em um espaço topológico \( X \), um conjunto \( A \) é aberto se e somente se coincide com o seu interior. Em outras palavras, \( A \) é aberto quando cada um de seus pontos possui uma vizinhança aberta inteiramente contida em \( A \). Formalmente, \( A = \operatorname{Int}(A) \) caracteriza exatamente os conjuntos abertos.
• Como calcular o interior de um conjunto em R
  A linguagem R é adequada para cálculos matemáticos e estatísticos, sendo útil também para a análise de interiores de conjuntos em espaços topológicos. Suas funções permitem calcular e visualizar esses interiores de maneira eficiente.

E assim por diante.