União dos interiores de dois conjuntos
A união dos interiores de dois conjuntos \( A \) e \( B \) está sempre contida no interior da união entre eles: \[ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) \] No entanto, essa inclusão nem sempre resulta em igualdade.
Em termos simples, o interior da união é sempre pelo menos tão amplo quanto a união dos interiores. Mas, na prática, esses dois conjuntos nem sempre coincidem. Isso significa que:
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
nem sempre é uma afirmação verdadeira. Em muitos casos, a inclusão é estrita:
$$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B) $$
Compreender essa diferença é essencial para entender como os conjuntos se comportam em um espaço topológico.
Exemplo ilustrativo
Vamos analisar dois intervalos abertos \( A \) e \( B \) em \(\mathbb{R}\), considerando a topologia usual:
$$ A = (0, 2) \qquad B = (1, 3) $$
O interior de um intervalo aberto é o próprio intervalo. Logo:
$$ \text{Int}(A) = (0, 2) \qquad \text{Int}(B) = (1, 3) $$
A união dos interiores é:
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 2) \cup (1, 3) = (0, 3) $$
Da mesma forma, a união dos conjuntos é:
$$ A \cup B = (0, 2) \cup (1, 3) = (0, 3) $$
Portanto, o interior da união coincide com a união dos interiores:
$$ \text{Int}(A \cup B) = (0, 3) $$
Neste caso, a igualdade é verificada.
Consideremos agora dois intervalos fechados: $$ A = [0, 2] \qquad B = [2, 3] $$ Seus interiores são: $$ \text{Int}(A) = (0, 2) \qquad \text{Int}(B) = (2, 3) $$ Já a união é \( A \cup B = [0, 3] \), e seu interior: $$ \text{Int}(A \cup B) = (0, 3) $$ A inclusão ainda vale: $$ (0, 2) \cup (2, 3) \subseteq (0, 3) $$ Mas a igualdade não ocorre, porque o ponto \( 2 \) pertence ao interior da união, mas não pertence a nenhum dos interiores individuais: $$ 2 \not\in \text{Int}(A), \quad 2 \not\in \text{Int}(B) $$ Assim: $$ \text{Int}(A) \cup \text{Int}(B) = (0, 2) \cup (2, 3) \ne (0, 3) $$ Esse exemplo mostra claramente que a inclusão pode ser estrita.
Exemplo 2
Consideremos agora dois intervalos abertos disjuntos:
$$ A = (0, 1) \qquad B = (2, 3) $$
Como são abertos, seus interiores coincidem com eles mesmos:
$$ \text{Int}(A) = (0, 1) \qquad \text{Int}(B) = (2, 3) $$
A união dos interiores é:
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 1) \cup (2, 3) $$
E, como a união de abertos é aberta, temos:
$$ \text{Int}(A \cup B) = (0, 1) \cup (2, 3) $$
Aqui também a igualdade é satisfeita.
Esses exemplos em \(\mathbb{R}\) mostram que a união dos interiores está sempre contida no interior da união. Porém, apenas certas configurações garantem igualdade. Quando há contato entre as fronteiras, a inclusão se torna estrita.
Exemplo 3
Consideremos agora dois conjuntos \( A \) e \( B \) no plano \(\mathbb{R}^2\), com a topologia usual.
Os conjuntos \( A \) e \( B \) são dois discos abertos que se sobrepõem parcialmente, centrados em \( (0, 0) \) e \( (0{,}5, 0) \), ambos com raio \( 1 \):
$$ A = \{ (x, y) \in \mathbb{R}^2 \mid x^2 + y^2 < 1 \} $$
$$ B = \{ (x, y) \in \mathbb{R}^2 \mid (x - 0{,}5)^2 + y^2 < 1 \} $$
Como são abertos, seus interiores são iguais aos próprios conjuntos:
$$ \text{Int}(A) = A \qquad \text{Int}(B) = B $$
A união dos interiores é a própria união dos discos:
$$ \text{Int}(A) \cup \text{Int}(B) = A \cup B $$
Essa união forma uma região contínua composta por dois discos com uma área de intersecção parcial.
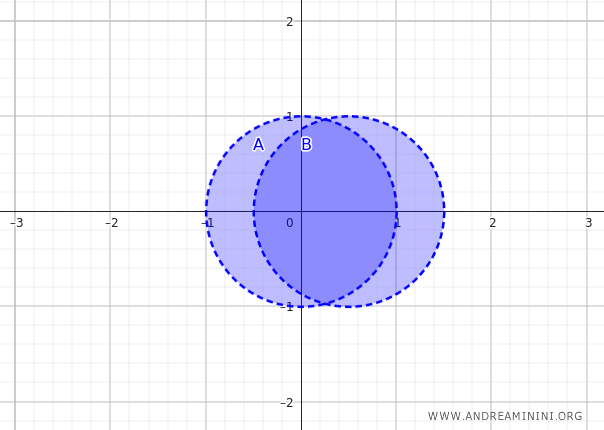
O interior da união \( A \cup B \) é o conjunto de todos os pontos que possuem uma vizinhança inteiramente contida em \( A \cup B \):
$$ \text{Int}(A \cup B) = A \cup B $$
Mais uma vez, verificamos a inclusão fundamental:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
Demonstração da propriedade
Para demonstrar essa propriedade, precisamos apenas mostrar que:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
Lembre-se da definição do interior de um conjunto:
O interior de um conjunto \( X \), denotado por \( \text{Int}(X) \), é o conjunto de todos os pontos \( x \in X \) para os quais existe um aberto que contém \( x \) e está completamente contido em \( X \).
Seja \( x \in \text{Int}(A) \cup \text{Int}(B) \). Então \( x \in \text{Int}(A) \) ou \( x \in \text{Int}(B) \).
- Se \( x \in \text{Int}(A) \), existe um aberto \( U_x \) tal que \( x \in U_x \subseteq A \).
- Se \( x \in \text{Int}(B) \), existe um aberto \( V_x \) tal que \( x \in V_x \subseteq B \).
Em ambos os casos, como \( A \subseteq A \cup B \) e \( B \subseteq A \cup B \), temos \( U_x \subseteq A \cup B \) ou \( V_x \subseteq A \cup B \). Assim, \( x \in \text{Int}(A \cup B) \).
Portanto, todo ponto de \( \text{Int}(A) \cup \text{Int}(B) \) também pertence a \( \text{Int}(A \cup B) \). Isso prova a inclusão desejada:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
A demonstração está, assim, concluída.