Conectividade em Topologia

Em topologia, um espaço é dito conexo quando não pode ser decomposto em abertos disjuntos. Em termos simples, a conectividade refere-se à possibilidade de unir quaisquer dois pontos do espaço por um caminho contínuo que permaneça dentro dos limites desse espaço.

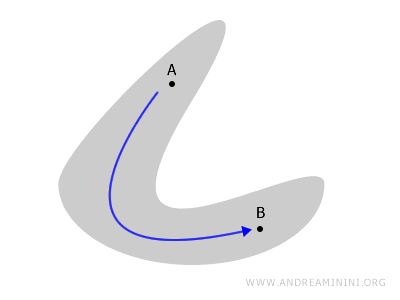
Conectividade descreve a forma como as partes de um espaço topológico estão interligadas ou, ao contrário, separadas entre si.

Esse conceito é um dos fundamentos da topologia, em estreita relação com a noção de continuidade.

A conectividade é central em diversas áreas da matemática, pois revela a estrutura interna dos espaços e as relações entre seus componentes. Ela é, por exemplo, uma ferramenta essencial para classificar e analisar espaços topológicos.

Um Exemplo Prático

Um espaço - seja ele uma figura plana ou um poliedro - é considerado conexo quando existe um caminho contínuo ligando quaisquer dois pontos A e B sem sair do espaço.

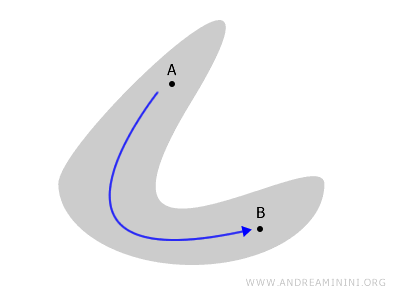
Por outro lado, se o espaço se divide em partes isoladas, ele deixa de ser conexo, sendo chamado de desconexo.

Nesse caso, o espaço está fragmentado em duas regiões disjuntas, e qualquer caminho que ligue A a B necessariamente sairia do espaço.

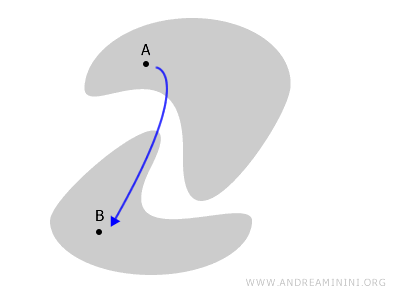
Vale aprofundar a ideia de espaços desconexos com outro exemplo concreto.

Quando um espaço é desconexo?

O exemplo mais intuitivo é imaginar dois cômodos distintos dentro de um mesmo edifício, separados por uma parede. Cada cômodo corresponde a um aberto; como as paredes (as fronteiras) não fazem parte do conjunto, esses abertos permanecem separados.

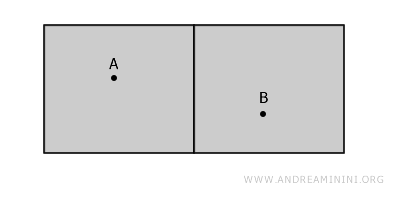
Apesar de os cômodos parecerem próximos, não estão conectados, pois qualquer caminho de A até B teria de atravessar a parede, que está fora do espaço considerado.

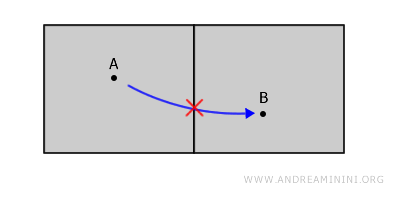
Em resumo: é fundamental lembrar que as fronteiras não pertencem a um conjunto aberto.

Conectividade Local

Há conectividade local quando, em torno de cada ponto do espaço, existe uma vizinhança conexa. Em outras palavras, cada ponto está contido em um subconjunto aberto que é conexo.

Retomando o exemplo dos dois cômodos de um edifício:

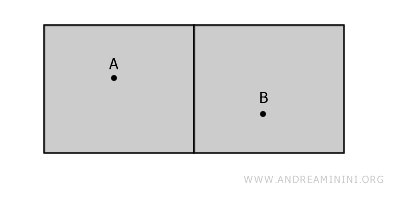
O espaço total é desconexo, pois não há caminho contínuo entre A e B sem atravessar a parede.

Porém, em torno do ponto A existe um aberto conexo que o contém, evidenciando conectividade local nesse ponto.

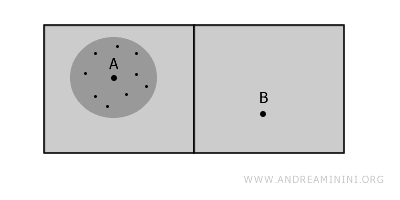
O mesmo raciocínio vale para o ponto B, que também possui conectividade local.

Tipos de Conectividade

Há diferentes formas de conectividade, mas duas se destacam pela importância:

• Conexão topológica
  Um espaço topológico $ X $ é dito conexo quando não é possível dividi-lo em dois conjuntos abertos, disjuntos e não vazios cuja união corresponda a todo o espaço. Em outras palavras, não há como “separar” o espaço em duas partes independentes.

  Exemplo. O intervalo (-1, 1) é conexo, enquanto o conjunto (-1, 0) ∪ (0, 1) não é, pois nele existem dois conjuntos abertos, disjuntos e não vazios (-1, 0) e (0, 1) cuja união cobre todo o espaço.
  Esses dois conjuntos formam, portanto, uma separação do espaço.

• Conexão por caminhos (ou por arcos)
  Diz-se que um espaço topológico é conexo por caminhos se, para qualquer par de pontos A e B pertencentes a esse espaço, existe um caminho contínuo que os liga e que permanece inteiramente dentro do próprio espaço. Todo espaço conexo por caminhos é também conexo, embora o contrário nem sempre seja verdadeiro.
  

  Por exemplo, imagine uma figura fechada no plano. Para quaisquer dois pontos interiores A e B, é possível traçar uma curva contínua que os conecte sem levantar o lápis do papel nem sair da região da figura.
  
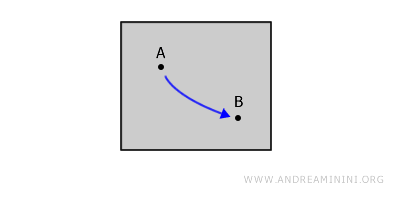
  Diferença entre conexão por arcos e por caminhos.  A conexão por arcos é semelhante à conexão por caminhos, mas nesse caso o caminho deve ser injetivo, isto é, não pode cruzar-se nem passar mais de uma vez pelo mesmo ponto.

• Conectividade Simples
  Um espaço é simplesmente conexo quando todo laço fechado pode ser continuamente contraído a um ponto. Isso equivale a dizer que o espaço não possui furos internos. Todo espaço simplesmente conexo é conexo, mas o inverso não se aplica em geral. Formalmente, em um espaço topológico simplesmente conexo, todo laço é homotópico a um ponto.
  

  A esfera é simplesmente conexa, pois qualquer laço em sua superfície pode ser reduzido a um ponto. Já a rosquinha, por ter um furo, é conexa mas não simplesmente conexa: existem laços que não podem ser contraídos.
  
  
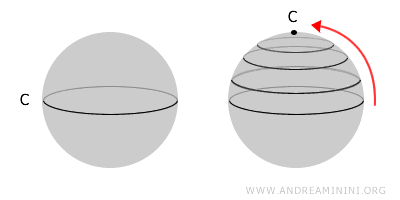
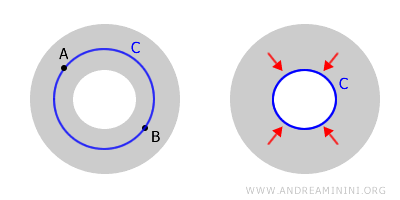
  Espaços conexos mas não simplesmente conexos recebem o nome de multiconexos. Um anel (ou coroa circular) é um exemplo típico desse tipo de conectividade.

Observações

Algumas observações importantes:

• No conjunto dos números reais, os únicos espaços conexos são os intervalos.