Todo subconjunto conexo está contido em uma única componente conexa do espaço
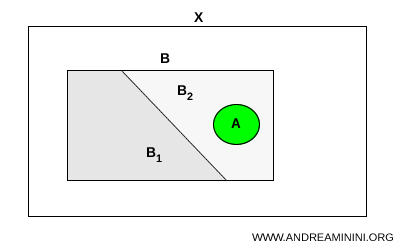
Sejam \( A \) e \( B \) dois subconjuntos de um espaço topológico \( X \). Suponha-se que \( A \) seja conexo e que \( A \subset B \). Se o conjunto \( B \) admite uma separação em dois subconjuntos \( B_1 \) e \( B_2 \) em \( X \), então \( A \) deve necessariamente estar inteiramente contido em apenas um deles: $$ A \subset B_1 \quad \text{ou} \quad A \subset B_2 $$
Em termos intuitivos, um subconjunto conexo não pode atravessar uma separação. Ele não pode tocar simultaneamente as duas partes em que um conjunto foi dividido.
Sempre que um subconjunto conexo está contido em um conjunto que se decompõe em duas partes disjuntas, ele não pode se espalhar entre elas. Ele deve permanecer integralmente em uma única parte.
Uma boa forma de visualizar essa ideia é pensar em um subconjunto conexo como uma corda contínua colocada dentro de um envelope. Se o envelope for dividido em dois compartimentos disjuntos, enquanto a corda permanece intacta, ela só poderá estar em um deles. Para ocupar ambos, seria necessário partir a corda. A conexidade expressa exatamente essa impossibilidade de "cortar" o conjunto ao atravessar uma separação.
Um exemplo concreto
Consideremos o seguinte espaço topológico:
$$ X = \mathbb{R} $$
e o subconjunto de \( X \):
$$ B = (-3,4) $$
Esse conjunto admite uma separação natural em dois subconjuntos:
$$ B_1 = (-3,0) $$
$$ B_2 = (0,4) $$
Esses dois subconjuntos são disjuntos:
$$ B_1 \cap B_2 = \varnothing $$
e sua reunião reconstrói exatamente o conjunto inicial:
$$ B_1 \cup B_2 = B $$
Além disso, \( B_1 \) e \( B_2 \) são abertos na topologia de subespaço induzida em \( B \).
Portanto, eles formam de fato uma separação de \( B \) no espaço \( X \).
Consideremos agora um subconjunto conexo de \( B \):
$$ A = (1,2) $$
É imediato observar que \( A \subset B_2 \). Assim, o subconjunto \( A \) está completamente contido em uma das duas partes da separação, exatamente como afirma o resultado geral.
Observação. Se, ao contrário, considerarmos \( A = (-1,1) \), obtemos $$ A \cap B_1 \neq \varnothing, \qquad A \cap B_2 \neq \varnothing $$ Essa situação não pode ocorrer, pois \( B_1 \) e \( B_2 \) constituem uma separação de \( B \). Um subconjunto conexo de \( B \) não pode estar distribuído entre as duas partes. Se isso fosse possível, então \( A \) admitiria ele próprio uma separação, o que contradiz o fato fundamental de que o intervalo \( (-1,1) \) é conexo. O ponto central não é uma perda de conexidade de \( (-1,1) \), mas a impossibilidade de esse intervalo estar contido em um conjunto separado dessa maneira.
Demonstração
Hipóteses
Sejam \( A \) e \( B \) subconjuntos de um espaço topológico \( X \).
$$ A \subset X \quad \text{e} \quad B \subset X $$
Suponha-se que:
- \( A \) é conexo
- \( A \subset B \)
- \( B_1 \) e \( B_2 \) formam uma separação de \( B \) no espaço \( X \)
Proposição
Nessas condições, o subconjunto \( A \) está contido em \( B_1 \) ou em \( B_2 \):
$$ A \subset B_1 \quad \text{ou} \quad A \subset B_2 $$
Demonstração
Pelas hipóteses, \( B_1 \) e \( B_2 \) constituem uma separação de \( B \) no espaço \( X \). Em particular, vale que:
- \( B_1 \cap B_2 = \varnothing \)
- \( B = B_1 \cup B_2 \)
- \( B_1 \) e \( B_2 \) são abertos na topologia de subespaço induzida em \( B \)
Suponhamos, por absurdo, que \( A \) não esteja inteiramente contido nem em \( B_1 \) nem em \( B_2 \). Nesse caso:
$$ A \cap B_1 \neq \varnothing \qquad \text{e} \qquad A \cap B_2 \neq \varnothing $$
Como \( A \subset B \), podemos escrever:
$$ A = A \cap B = A \cap (B_1 \cup B_2) = (A \cap B_1) \cup (A \cap B_2) $$
Os conjuntos \( A \cap B_1 \) e \( A \cap B_2 \) são disjuntos, pois \( B_1 \) e \( B_2 \) também o são.
Além disso, como \( B_1 \) e \( B_2 \) são abertos em \( B \), os conjuntos \( A \cap B_1 \) e \( A \cap B_2 \) são abertos na topologia de subespaço induzida em \( A \).
Dessa forma, \( A \cap B_1 \) e \( A \cap B_2 \) constituem dois subconjuntos disjuntos, não vazios e abertos de \( A \). Eles definem, portanto, uma separação de \( A \).
Isso contradiz a hipótese de que \( A \) é conexo.
Conclui-se, portanto, que a suposição inicial é falsa, obtendo-se:
$$ A \subset B_1 \quad \text{ou} \quad A \subset B_2 $$
A proposição fica, assim, demonstrada.
E assim por diante.