Espaços Conexos por Caminho

Um espaço topológico S é dito conexo por caminho quando existe uma trajetória contínua ligando quaisquer dois pontos A e B dentro do espaço, sem jamais sair dele.

Imagine uma folha de papel, desconsiderando suas bordas.

Ela representa uma região contínua única e é considerada aberta, já que as fronteiras não estão incluídas.

Para quaisquer dois pontos A e B sobre a folha, é sempre possível traçar uma linha contínua com uma caneta sem levantar a ponta do papel.

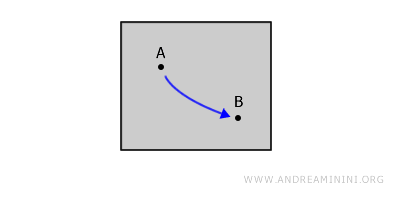
Em outras palavras, o caminho permanece inteiramente contido no espaço que contém A e B.

Todo espaço conexo por caminho é, necessariamente, um espaço conexo.

Isso parece imediato: se um espaço fosse desconexo, estaria dividido em partes separadas, e não haveria como unir dois pontos por um caminho contínuo sem sair dele.

No entanto, o recíproco não vale. Nem todo espaço conexo é conexo por caminho.

Vejamos um exemplo que, embora contraintuitivo, é perfeitamente válido.

Consideremos dois conjuntos, Q e T:

$$ Q = \{ \forall \ x \ \in \mathbb{R}-\{ 0 \} \ , \ \sin\!\left(\tfrac{1}{x}\right) \} $$

$$ T = \{ 0 \} $$

O primeiro conjunto, Q, é formado por todos os pontos da curva do seno definidos para os reais, exceto em zero, onde a função não está definida por envolver divisão por zero.

O segundo conjunto, T, contém apenas o ponto 0.

Os conjuntos Q e T estão infinitamente próximos, como ilustra o gráfico da função contínua sen(1/x).

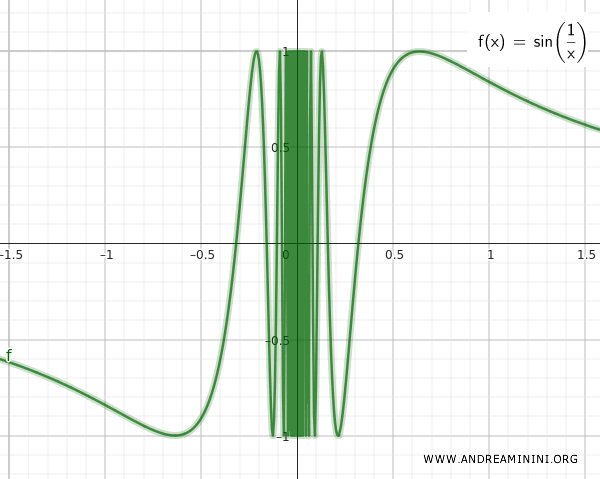
Definimos S como a união de Q e T:

$$ S = Q \cup T $$

O conjunto S é conexo porque, para qualquer ε>0, existe uma vizinhança em torno de zero (0-ε, 0+ε) que contém pontos de Q.

Isso ocorre porque 0 é um ponto de acumulação da função sen(1/x).

Apesar disso, S não é conexo por caminho, pois não existe trajetória contínua que una um ponto de Q ao ponto 0 (conjunto T).

Observação: A situação seria diferente se considerássemos f(x)=1/x. Nesse caso, é evidente que Q e T são disjuntos e não estão infinitamente próximos.

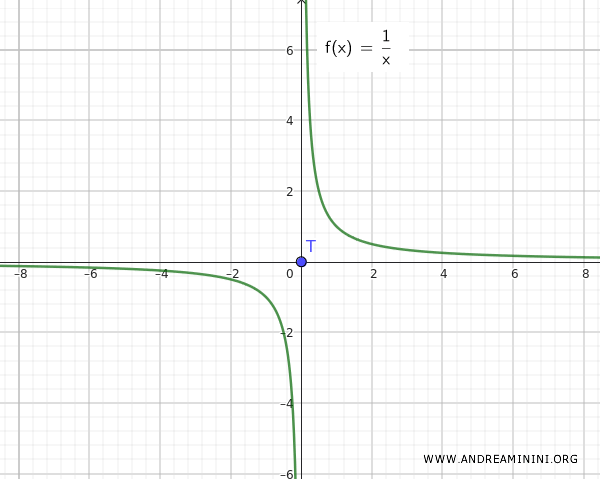
Esse exemplo mostra que a união de um conjunto conexo Q={∀ x ∈ R-{0}, 1/x} com um ponto isolado T={0} não resulta necessariamente em um espaço conexo, a menos que esse ponto isolado (como o 0) também seja um ponto de acumulação.

 E assim por diante.