Espaços Simplesmente Conexos em Topologia

Um espaço topológico é simplesmente conexo quando todo caminho fechado nele pode ser continuamente deformado até se contrair em um único ponto.

De forma mais intuitiva, um espaço é simplesmente conexo se qualquer laço puder ser reduzido a um ponto sem sair do próprio espaço.

Isso caracteriza um espaço como um “bloco único” (isto é, conexo), sem a presença de “furos internos”.

Observação: Todo espaço simplesmente conexo é, portanto, também conexo. O contrário, porém, não é verdadeiro: nem todo espaço conexo é simplesmente conexo.

Um Exemplo Prático

A esfera é um exemplo clássico de espaço simplesmente conexo: qualquer curva fechada sobre sua superfície pode ser continuamente contraída até um ponto.

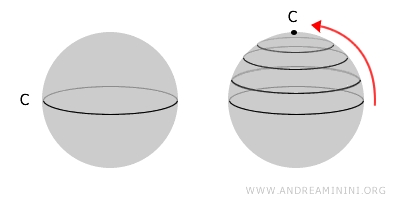
Já o toro - a conhecida “rosquinha” - não é simplesmente conexo, devido ao furo central, que impede que certos laços possam ser reduzidos a um ponto.

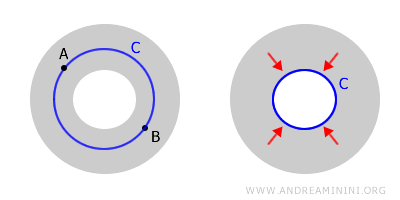
Esse contraste evidencia que a conectividade, por si só, não garante a simples conectividade.

O toro é um espaço conexo, pois quaisquer dois pontos A e B podem ser unidos por um caminho contido em sua superfície.

No entanto, não é simplesmente conexo, já que existem laços que não podem ser continuamente contraídos.

Quando um espaço é conexo, mas não simplesmente conexo, ele é classificado como multiconexo. Exemplos típicos incluem a região anular e o espaço toroidal.

Assim, a simples conectividade é uma condição mais forte do que a conectividade por caminho.

E assim por diante.