O que é um Espaço Conexo?
Entendendo a definição com conjuntos abertos
Um espaço topológico $ X $ é chamado de conexo quando não é possível dividi-lo em duas partes abertas, não vazias e que não se tocam entre si.
- $ U \neq \emptyset $ e $ V \neq \emptyset $ - ambos contêm pelo menos um ponto;
- $ U \cap V = \emptyset $ - eles não compartilham nenhum ponto;
- $ U \cup V \ne X $ - juntos, não cobrem o espaço todo.
Se, pelo contrário, existirem dois conjuntos abertos $ U $ e $ V $ com essas características, dizemos que o espaço é desconexo.
Em outras palavras, um espaço é conexo quando não conseguimos "quebrá-lo" em duas regiões abertas que fiquem completamente separadas. Quando isso acontece, dizemos que o par $(U, V)$ forma uma separação de $(X)$.
Nota. Esta é a definição de conexidade topológica em termos de conjuntos abertos. Mais adiante veremos que ela não é a mesma coisa que "conexidade por caminhos" - duas ideias parecidas, mas não idênticas.
Um exemplo simples
Vamos começar com um caso pequeno e fácil de visualizar. Considere o conjunto $ X $ com três elementos:
$$ X = \{a, b, c\} $$
Sobre ele, definimos duas topologias diferentes:
- Topologia A
$$ \mathcal{T}_A = \{ \emptyset, X, \{ a,b \}, \{ b \}, \{ b,c \} \} $$ - Topologia B
$$ \mathcal{T}_B = \{ \emptyset, X, \{ a,b \}, \{ c \}, \{ b,c \} \} $$
Agora vem a pergunta: qual dos dois espaços é conexo?
Pela definição, o espaço é conexo se não houver dois conjuntos abertos, não vazios e disjuntos, cuja união cubra todo $ X $.
1] Topologia A
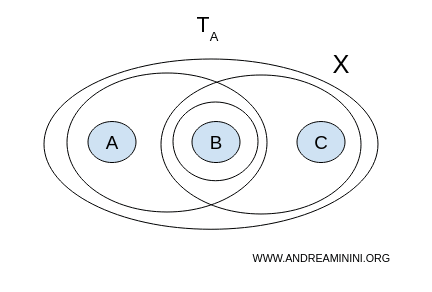
Vamos procurar um par de conjuntos abertos $ (U, V) $ em $ \mathcal{T}_A $ que satisfaça as condições de uma separação:
- $ U = \{a,b\}, V = \{b,c\} $ → não são disjuntos (ambos contêm $ b $);
- $ U = \{a,b\}, V = \{b\} $ → também não são disjuntos;
- $ U = \{b\}, V = \{b,c\} $ → idem.
Nenhum par funciona. Portanto, com a topologia $ A $, o espaço $ X $ é conexo.
2] Topologia B
Agora testemos a segunda topologia:
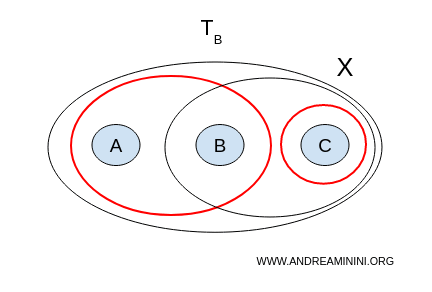
- $ U = \{a,b\}, V = \{b,c\} $ → novamente não são disjuntos;
- $ U = \{a,b\}, V = \{c\} $ → são disjuntos, não vazios e cobrem todo o espaço: $ U \cup V = \{a,b,c\} = X $.
Perfeito: encontramos uma separação. Logo, o espaço $ X $ com a topologia B é desconexo.
Nota. Veja como a escolha da topologia faz toda a diferença: o mesmo conjunto de pontos pode ser conexo ou desconexo dependendo de quais subconjuntos consideramos abertos.
Outro exemplo: a reta real sem um ponto
Considere agora o conjunto
$$ X = (-\infty, n) \cup (n, +\infty) $$
onde $ n $ é um número real fixo (por exemplo, $ n = 0 $). Este espaço representa a reta real sem o ponto $ n $:
$$ X = \mathbb{R} \setminus \{n\} $$
Os conjuntos $ U = (-\infty, n) $ e $ V = (n, +\infty) $ são:
- abertos na topologia usual de $ \mathbb{R} $;
- não vazios;
- e disjuntos (não compartilham pontos).
Além disso, $ U \cup V = X $. Tudo se encaixa na definição de separação. Conclusão: o espaço $ X = (-\infty, n) \cup (n, +\infty) $ é desconexo.
Nota. Remover um único ponto da reta real é o suficiente para "quebrar" sua continuidade. A reta se divide em duas partes - uma à esquerda e outra à direita de $ n $ - que não podem mais ser ligadas por nenhum caminho contínuo. Por isso, o espaço é desconexo e também não conexo por caminhos.
Conexo x Conexo por Caminhos
É comum confundir essas duas ideias, mas elas não são a mesma coisa. Um espaço pode ser conexo e, ainda assim, não ser conexo por caminhos.
- Conexidade topológica
O espaço não pode ser dividido em dois abertos disjuntos e não vazios cuja união seja o espaço inteiro. - Conexidade por caminhos
Para quaisquer dois pontos do espaço, existe um caminho contínuo dentro dele que liga um ao outro. Se o caminho não se repete, o espaço é dito conexo por arcos.
De forma geral, todo espaço conexo por caminhos é conexo, mas o contrário não é sempre verdade.
Um caminho contínuo garante que o espaço não pode ser "cortado" em duas regiões abertas separadas. Mas é possível ter um espaço que seja conexo, embora não exista caminho contínuo ligando certos pontos.
Exemplo. Um caso clássico é a curva do seno do topólogo:
$$ S = \{ (x, \sin(1/x)) \mid x > 0 \} \cup \{ (0, y) \mid -1 \le y \le 1 \} $$
Esse espaço é conexo - não pode ser dividido em dois abertos disjuntos - , mas não é conexo por caminhos, porque não há caminho contínuo que una um ponto da curva oscilante a um ponto do segmento vertical.
Notas
Observações complementares sobre espaços conexos
- Teorema: caracterização dos espaços conexos por conjuntos abertos e fechados (clopen)
Um espaço topológico \( X \) é dito conexo se, e somente se, os únicos subconjuntos de \( X \) que são simultaneamente abertos e fechados (clopen) são o próprio \( X \) e o conjunto vazio \( \emptyset \).
Outras propriedades e exemplos podem ser estudados a partir desse princípio fundamental.