Teorema: como reconhecer se um espaço é conexo usando conjuntos abertos e fechados (clopen)

Um espaço topológico \( X \) é chamado conexo quando os únicos subconjuntos que são ao mesmo tempo abertos e fechados (também conhecidos como clopen) são o próprio \( X \) e o conjunto vazio \( \emptyset \).

Em outras palavras, o espaço é conexo se não houver subconjuntos próprios e não vazios que possuam, ao mesmo tempo, as duas propriedades: serem abertos e fechados (clopen).

Esse resultado oferece um critério simples e poderoso para verificar a conectividade topológica de um espaço, sem precisar recorrer a ideias mais complexas, como a conectividade por caminhos.

Por que isso importa

Em topologia, um conjunto que é aberto e fechado ao mesmo tempo divide o espaço em duas partes separadas: dois conjuntos abertos, disjuntos e não vazios. Isso significa que o espaço "se parte em dois pedaços" que não se tocam.

Se tal conjunto clopen existir e for diferente de \( X \) e de \( \emptyset \), o espaço pode ser descrito como a união de dois abertos disjuntos e não vazios. Nesse caso, o espaço é não conexo (ou desconexo).

Se, por outro lado, os únicos conjuntos clopen de \( X \) forem \( X \) e \( \emptyset \), não há como separá-lo dessa forma. Logo, o espaço é conexo.

Observação. Em qualquer espaço topológico, o conjunto total \( X \) e o conjunto vazio \( \emptyset \) são sempre abertos e fechados.

Exemplo 1: um espaço finito desconexo

Vamos considerar \( X = \{ a, b, c, d \} \) com a topologia \( T \) formada pelos abertos \( \{ b \}, \{ a, b \}, \{ c, d \}, \{ b, c, d \}, \{ a, b, c, d \}, \emptyset \).

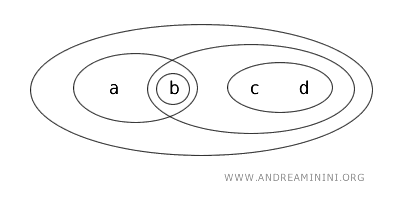
Nesse espaço, o conjunto \( \{ a, b \} \) é clopen porque:

• É aberto: ele aparece explicitamente entre os abertos da topologia \( T \).
• É fechado: o seu complemento \( X \setminus \{ a, b \} = \{ c, d \} \) também é aberto em \( T \).

Isso mostra que o espaço \( (X, T) \) é desconexo, já que possui um subconjunto próprio e não vazio que é clopen.

Basta a existência de um único conjunto clopen não trivial para concluir que o espaço não é conexo. Nesse caso, o espaço pode ser decomposto em dois abertos disjuntos e não vazios, \( \{ a, b \} \) e \( \{ c, d \} \), o que viola a condição de conectividade topológica.

Exemplo 2: o espaço dos números reais

Agora, consideremos o conjunto dos números reais \( \mathbb{R} \) com a topologia usual, gerada pelos intervalos abertos \( (a, b) \).

Nessa topologia, os intervalos \( (a, b) \) são abertos, mas não fechados, enquanto os intervalos \( [a, b] \) são fechados, mas não abertos.

Os únicos subconjuntos de \( \mathbb{R} \) que são ao mesmo tempo abertos e fechados são \( \mathbb{R} \) e \( \emptyset \).

Logo, o espaço dos números reais com a topologia usual é conexo. Não existe nenhuma forma de separá-lo em duas partes abertas e disjuntas.

Exemplo 3: um subespaço desconexo de \( \mathbb{R} \)

Consideremos agora o subespaço \( X = (0,1) \cup (2,3) \subset \mathbb{R} \), com a topologia de subespaço induzida pela topologia usual.

Aqui, os intervalos \( (0,1) \) e \( (2,3) \) são simultaneamente abertos e fechados em \( X \), pois o complemento de cada um dentro de \( X \) é justamente o outro intervalo. Veja:

• O complemento de \( (0,1) \) em \( X \) é \( (2,3) \), que é aberto em \( X \).
• O complemento de \( (2,3) \) em \( X \) é \( (0,1) \), que também é aberto em \( X \).

Ambos são, portanto, conjuntos clopen.

Como há subconjuntos não triviais que são ao mesmo tempo abertos e fechados, o subespaço \( X \) é desconexo.

Isso acontece porque \( X \) pode ser visto como a união de dois abertos disjuntos e não vazios, \( (0,1) \) e \( (2,3) \), que juntos formam todo o espaço.