Espaços Regulares em Topologia
Chamamos de regular um espaço topológico \( X \) que satisfaz duas condições essenciais:
- Todo conjunto unitário é fechado. Para cada \( x \in X \), o conjunto \(\{x\}\) é fechado.
- Pontos e conjuntos fechados podem ser separados. Se \( a \in X \) e \( C \subset X \) é um conjunto fechado que não contém \( a \), então existem abertos disjuntos \( U \) e \( V \) tais que: \[ a \in U, \quad C \subset V, \quad U \cap V = \emptyset. \]
Em Topologia, a noção de regularidade expressa um tipo específico de separação. Ela exige mais do que a condição de Hausdorff, na qual apenas pontos distintos precisam ser separados por abertos.
Quando um espaço regular possui ainda uma base enumerável, o teorema de Urysohn assegura que ele é metrizável, isto é, sua topologia pode ser obtida a partir de uma métrica.
Comparação com Espaços de Hausdorff
A regularidade afirma que sempre é possível separar um ponto e um conjunto fechado disjunto por abertos independentes entre si. Já nos espaços de Hausdorff, a separação garantida é apenas entre pontos distintos. Isso mostra que todo espaço regular tem um poder de distinção mais forte.
Nota. Regularidade e normalidade não são sinônimos. Em um espaço normal, qualquer par de conjuntos fechados disjuntos pode ser separado por abertos disjuntos, o que é uma exigência mais forte. Assim, todo espaço normal é regular, mas nem todo espaço regular é normal.
Essas propriedades fazem parte da hierarquia dos axiomas de separação. Existem espaços de Hausdorff que não são regulares e espaços regulares que não são de Hausdorff, o que mostra que as duas condições são logicamente independentes.
Exemplo Prático em \( \mathbb{R} \)
Um exemplo claro de espaço regular é a reta real \( \mathbb{R} \) com a topologia padrão. Considere um ponto \( x \in \mathbb{R} \) e um conjunto fechado \( C \) que não o contém.
Tomemos, por exemplo, \( x = 2 \) e:
\[ C = (-\infty, 0] \cup [5, \infty) \]
É fácil verificar que \( 2 \notin C \) e que \( C \) é fechado na topologia usual.

Para mostrar a regularidade, buscamos abertos que separem o ponto \( x \) do conjunto \( C \). O complemento de \( C \) é aberto e contém o intervalo \( (0,5) \), que funciona como vizinhança de \( x = 2 \):
\[ (a, b) = (0, 5) \]
Escolhemos então valores \( c \) e \( d \) tais que:
\[ 0 < c < 2 < d < 5 \]
Por exemplo, \( c = 1 \) e \( d = 3 \).
Definimos os abertos:
- \( U = (1,3) \), vizinhança do ponto \( 2 \).
- \( V = (-\infty, 1) \cup (3, \infty) \), aberto que contém o conjunto \( C \).
Como \( U \cap V = \emptyset \), os conjuntos encontrados realizam exatamente a separação exigida pela definição de regularidade.
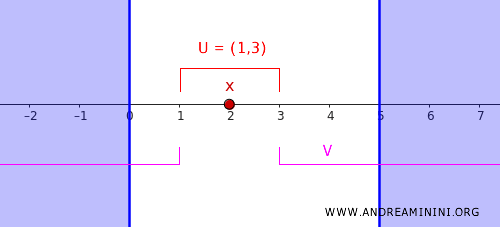
Concluímos que \( \mathbb{R} \), com a topologia usual, é regular porque sempre podemos isolar qualquer ponto de um conjunto fechado disjunto por meio de abertos separados.
Para Guardar na Memória
Ideias essenciais sobre espaços regulares:
- Axiomas de separação
A regularidade e a condição de Hausdorff pertencem à família dos axiomas de separação, que medem o grau de precisão com que um espaço distingue seus elementos. Quanto mais forte o axioma, maior o poder de separação.Nota. Em termos intuitivos, ser Hausdorff significa separar pontos. Ser regular significa separar um ponto de um conjunto fechado que não o contém. São níveis diferentes de resolução topológica.
E assim por diante.