Teorema do Interior de um Produto Cartesiano

Sejam \(A\) e \(B\) subconjuntos contidos, respectivamente, nos espaços topológicos \(X\) e \(Y\). O interior do produto cartesiano \(A \times B\) coincide com o produto dos interiores de \(A\) e \(B\). Em notação matemática: $$ \text{Int}(A \times B) = \text{Int}(A) \times \text{Int}(B) $$

Esse resultado é particularmente relevante no estudo da topologia produto, especialmente quando \(A\) e \(B\) são conjuntos abertos. Ele descreve como a operação de interior se comporta em relação ao produto cartesiano, fornecendo uma relação simples e intuitiva.

Em termos conceituais, o teorema afirma que não surgem novos pontos interiores ao formar o produto cartesiano. Os pontos interiores de \(A \times B\) são exatamente aqueles obtidos combinando pontos interiores de \(A\) com pontos interiores de \(B\).

Um exemplo concreto

Consideremos os espaços topológicos \(X = \mathbb{R}\) e \(Y = \mathbb{R}\), e os subconjuntos \(A = (0, 2)\) e \(B = (1, 3)\).

Ambos são intervalos abertos da reta real \(\mathbb{R}\). Isso torna o exemplo particularmente simples e geométrico.

Comecemos determinando o interior de cada conjunto.

Como \(A\) já é aberto, o seu interior coincide com o próprio conjunto:

$$ \text{Int}(A) = (0, 2) $$

De forma análoga, para o conjunto \(B\), temos:

$$ \text{Int}(B) = (1, 3) $$

Passemos agora ao produto dos interiores.

$$ \text{Int}(A) \times \text{Int}(B) = (0, 2) \times (1, 3) $$

Esse conjunto é formado por todos os pares ordenados \((x, y)\) tais que \(x\) pertence ao intervalo \((0, 2)\) e \(y\) pertence ao intervalo \((1, 3)\):

$$ \{(x, y) \mid x \in (0, 2),\ y \in (1, 3)\} $$

Geometricamente, trata-se de um retângulo aberto no plano \(\mathbb{R}^2\), delimitado pelos pontos \((0, 1)\), \((0, 3)\), \((2, 1)\) e \((2, 3)\), sem incluir suas bordas.

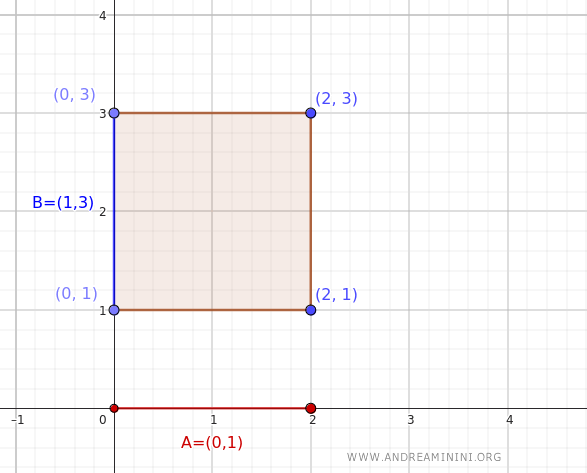
Analisemos agora o interior do produto cartesiano \(A \times B = (0, 2) \times (1, 3)\).

Como o produto de dois conjuntos abertos é aberto na topologia produto, o interior de \(A \times B\) coincide com o próprio conjunto. Mais uma vez, obtemos um retângulo aberto em \(\mathbb{R}^2\).

Assim, verificamos explicitamente que:

$$ \text{Int}(A \times B) = (0, 2) \times (1, 3) = \text{Int}(A) \times \text{Int}(B) $$

Esse exemplo ilustra de maneira direta e visual a validade do teorema.

Demonstração

A demonstração baseia-se em uma dupla inclusão. Primeiro mostramos que o produto dos interiores está contido no interior do produto. Em seguida, demonstramos a inclusão inversa. A combinação dessas duas etapas leva à igualdade desejada.

1] O produto dos interiores está contido no interior do produto

Queremos provar que:

$$ \text{Int}(A) \times \text{Int}(B) \subseteq \text{Int}(A \times B) $$

Seja \((x, y)\) um par tal que \(x \in \text{Int}(A)\) e \(y \in \text{Int}(B)\).

Por definição de interior, existe um aberto \(U \subseteq X\) com \(x \in U \subseteq A\), e um aberto \(V \subseteq Y\) com \(y \in V \subseteq B\).

O produto \(U \times V\) é um aberto de \(X \times Y\) que contém o ponto \((x, y)\) e está contido em \(A \times B\).

Portanto, \((x, y)\) é um ponto interior de \(A \times B\), o que prova a inclusão desejada.

2] O interior do produto está contido no produto dos interiores

Mostremos agora que:

$$ \text{Int}(A \times B) \subseteq \text{Int}(A) \times \text{Int}(B) $$

Se \((x, y)\) é um ponto interior de \(A \times B\), então existe um aberto \(W \subseteq X \times Y\) tal que \((x, y) \in W \subseteq A \times B\).

Pela definição da topologia produto, podemos supor que existe um aberto básico \(U \times V\) com \((x, y) \in U \times V \subseteq W\), onde \(U \subseteq X\) e \(V \subseteq Y\) são abertos.

Da inclusão \(U \times V \subseteq A \times B\) segue-se que \(U \subseteq A\) e \(V \subseteq B\). Assim, \(x \in \text{Int}(A)\) e \(y \in \text{Int}(B)\).

Logo, \((x, y)\) pertence a \(\text{Int}(A) \times \text{Int}(B)\), o que estabelece a segunda inclusão.

3] Conclusão

Como demonstramos que:

$$ \text{Int}(A) \times \text{Int}(B) \subseteq \text{Int}(A \times B) $$

e

$$ \text{Int}(A \times B) \subseteq \text{Int}(A) \times \text{Int}(B), $$

concluímos que:

$$ \text{Int}(A \times B) = \text{Int}(A) \times \text{Int}(B). $$

Isso conclui a demonstração do teorema.