Conjuntos Clopen
Un conjunto se dice "clopen" si es simultáneamente abierto y cerrado dentro de una determinada topología.
En otras palabras, un conjunto clopen satisface, al mismo tiempo, las condiciones para ser abierto y cerrado en la topología considerada.
El término "clopen" proviene de la fusión de las palabras "closed" (cerrado) y "open" (abierto).
Estos conjuntos presentan propiedades tanto de los conjuntos abiertos como de los conjuntos cerrados.
Esto ocurre cuando tanto un conjunto como su complemento son abiertos en la topología dada.
Nota: Los conjuntos clopen son poco frecuentes en los números reales, pero aparecen en otros espacios topológicos. Son especialmente interesantes porque exhiben propiedades singulares y desempeñan un papel clave en el estudio de la estructura topológica de un espacio.
Un Ejemplo Práctico
Consideremos el conjunto \(X=\{a,b,c,d\}\) en una topología \(T\).
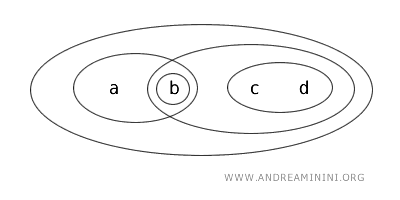
Bajo la topología \(T\), los conjuntos considerados abiertos son: \(\{b\}, \{a,b\}, \{c,d\}, \{b,c,d\}, \{a,b,c,d\}, \varnothing\).
Por lo tanto, el subconjunto \(\{a,b\}\) es un conjunto abierto en esta misma topología \(T\).
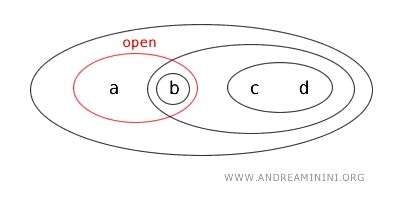
Curiosamente, el conjunto \(\{a,b\}\) también es el complemento del conjunto abierto \(\{c,d\}\):
$$ X - \{ c,d \} = \{a , b \} $$
Dado que el complemento de un conjunto abierto es siempre un conjunto cerrado:
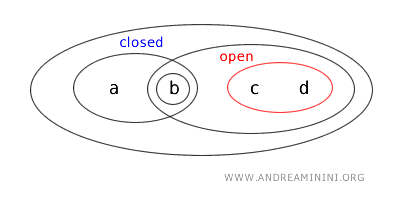
Se concluye que el conjunto \(\{a,b\}\) también es un conjunto cerrado.
En definitiva, dentro de la topología \(T\), el conjunto \(\{a,b\}\) es a la vez abierto y cerrado, lo que lo convierte en un conjunto clopen.
El Conjunto Vacío y el Conjunto Total son Clopen
En cualquier topología sobre un conjunto \(X\), tanto el conjunto total (\(X\)) como el conjunto vacío (\(\varnothing\)) son siempre clopen, es decir, simultáneamente abiertos y cerrados.
Un conjunto se considera clopen si cumple simultáneamente con las definiciones de conjunto abierto y conjunto cerrado dentro de la topología en cuestión.
Revisemos brevemente las definiciones de conjunto abierto y cerrado para comprender mejor este concepto.
De acuerdo con la definición topológica de conjunto abierto, tanto el conjunto vacío (\(\varnothing\)) como el conjunto total (\(X\)) son siempre abiertos.
Asimismo, según la definición de conjunto cerrado, un conjunto se considera cerrado si su complemento es un conjunto abierto.
A partir de estas definiciones, podemos deducir lo siguiente:
- Conjunto vacío (\(\varnothing\))
Por los axiomas básicos de la topología, el conjunto vacío es abierto. Al mismo tiempo, es cerrado, ya que su complemento, \(X \setminus \varnothing = X\) (el conjunto total), es un conjunto abierto. Por lo tanto, el conjunto vacío es a la vez abierto y cerrado, es decir, clopen. - Conjunto total (\(X\))
El conjunto total es abierto por definición topológica. A su vez, es cerrado, ya que su complemento, \(X \setminus X = \varnothing\) (el conjunto vacío), es un conjunto abierto. En consecuencia, el conjunto total también es clopen.
Por lo tanto, en cualquier topología, tanto el conjunto total \(X\) como el conjunto vacío \(\varnothing\) son conjuntos clopen.
Y así sucesivamente.