Ejercicio 41. Evaluación de una integral indefinida

Calculemos la integral:

$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx $$

La integranda es una función racional propia, ya que el grado del numerador es menor que el del denominador. Por ello, no hace falta realizar una división de polinomios y podemos aplicar directamente la descomposición en fracciones parciales.

El denominador se anula en $ x = -1 $, que es un cero simple, y en $ x = -3 $, que es un cero doble. En consecuencia, planteamos:

$$ \frac{2x+5}{(x+1)(x+3)^2} = \frac{A}{x+1} + \frac{B}{x+3} + \frac{C}{(x+3)^2} $$

Llevamos todo a un denominador común:

$$ \frac{A(x+3)^2 + B(x+1)(x+3) + C(x+1)}{(x+1)(x+3)^2} $$

Desarrollamos el numerador:

$$ A(x^2 + 6x + 9) + B(x^2 + 4x + 3) + Cx + C $$

Agrupamos términos semejantes:

$$ (A + B)x^2 + (6A + 4B + C)x + (9A + 3B + C) $$

Como los denominadores coinciden, igualamos los numeradores:

$ 2x + 5 = (A + B)x^2 + (6A + 4B + C)x + (9A + 3B + C) $

Al comparar coeficientes de potencias de $ x $, obtenemos el sistema:

Coeficiente de $ x^2 $: $ A + B = 0 $
Coeficiente de $ x $: $ 6A + 4B + C = 2 $
Término independiente: $ 9A + 3B + C = 5 $

Explicación. La igualdad entre polinomios exige que coincidan sus coeficientes. En el primer miembro no aparece el término en $ x^2 $, por lo que su coeficiente es 0.
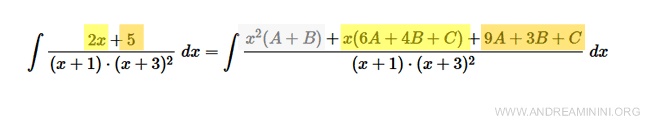
$igualación de coeficientes en la descomposición en fracciones parciales$

Resolvemos el sistema. De $ A + B = 0 $ se deduce $ A = -B $. Sustituimos:

$$ \begin{cases} -2B + C = 2 \\ -6B + C = 5 \end{cases} $$

Restamos ambas ecuaciones:

$ (-6B + C) - (-2B + C) = 5 - 2 \Rightarrow -4B = 3 \Rightarrow B = -\frac{3}{4} $

Entonces:

$ A = \frac{3}{4} $, $ C = 2 + 2B = 2 - \frac{3}{2} = \frac{1}{2} $

Con ello:

A = 3/4, B = -3/4, C = 1/2.

Sustituimos en la integral:

$$ \int \frac{2x+5}{(x+1)(x+3)^2} \ dx = \int \left( \frac{3}{4(x+1)} - \frac{3}{4(x+3)} + \frac{1}{2(x+3)^2} \right) dx $$

Por la linealidad de la integral:

$$ = \frac{3}{4} \int \frac{1}{x+1} \ dx - \frac{3}{4} \int \frac{1}{x+3} \ dx + \frac{1}{2} \int \frac{1}{(x+3)^2} \ dx $$

Integramos término a término:

$ \int \frac{1}{x+1} \ dx = \ln|x+1| + C $
$ \int \frac{1}{x+3} \ dx = \ln|x+3| + C $
$ \int \frac{1}{(x+3)^2} \ dx = -\frac{1}{x+3} + C $

Finalmente:

$$ \int \frac{2x+5}{(x+1)(x+3)^2} \ dx = \frac{3}{4} \ln|x+1| - \frac{3}{4} \ln|x+3| - \frac{1}{2(x+3)} + C $$

Nota. El último término se obtiene mediante la regla de la potencia: $$ \frac{d}{dx}\left[-(x+3)^{-1}\right] = \frac{1}{(x+3)^2} $$

Resultado:

$$ \int \frac{2x+5}{(x+1)(x+3)^2} \ dx = \frac{3}{4} \ln|x+1| - \frac{3}{4} \ln|x+3| - \frac{1}{2(x+3)} + C $$

Con esto queda resuelta la integral.