Integración de funciones racionales mediante fracciones parciales
La descomposición en fracciones parciales es una de las herramientas más utilizadas para integrar funciones racionales del tipo $$ \int \frac{P(x)}{Q(x)} $$ donde \( P(x) \) y \( Q(x) \) son polinomios, y el grado del numerador es menor o igual que el del denominador.
Cuando el numerador \( P_n(x) \) tiene grado \( n \leq m \), siendo \( m \) el grado del denominador \( Q(x) \), la integral se escribe simplemente como $$ \int \frac{P(x)_n}{Q(x)_m} \ dx $$
Nota. Si el grado del numerador es mayor que el del denominador, siempre es posible aplicar una división polinómica para reducir la expresión a una forma equivalente en la que el grado del numerador no lo supere. Una vez hecho esto, el método de fracciones parciales puede aplicarse sin dificultad.
La forma concreta de la descomposición depende del tipo de raíces del denominador \( Q(x) \): pueden ser reales simples, reales múltiples o complejas.
- Caso 1: el denominador se factoriza en los números reales. Esto ocurre cuando puede escribirse como producto de factores lineales del tipo \( (x - a) \), \( (x - a)^n \) o, de forma equivalente, expresiones como \( ax + b \). Por ejemplo, \( 3(x - 2) = 3x - 6 \).
- A cada factor lineal simple \( x - a \) le corresponde una fracción parcial de la forma $$ \frac{A}{x - a} $$
- Si el factor está repetido, como en \( (x - a)^n \), la descomposición incluye una suma de términos con potencias crecientes en el denominador: $$ \frac{A}{x - a} + \frac{B}{(x - a)^2} + \dots + \frac{C}{(x - a)^n} $$
Nota. Todo polinomio cuadrático de la forma \( ax^2 + bx + c \) con discriminante \( \Delta \geq 0 \) admite una factorización real del tipo \( a(x - x_1)(x - x_2) \), donde \( x_1 \) y \( x_2 \) son sus raíces. Para más detalles, véase factorización de trinomios cuadráticos.
- Caso 2: el denominador contiene factores cuadráticos irreducibles. Esto sucede cuando aparecen polinomios con raíces complejas conjugadas, es decir, cuando \( \Delta < 0 \). Ejemplos habituales son \( x^2 + 1 \) o \( (x^2 + 1)^n \).
- Cada factor cuadrático irreducible da lugar a una fracción parcial de la forma $$ \frac{Ax + B}{ax^2 + bx + c} $$
- Si el factor es múltiple, la descomposición adopta la estructura general: $$ \frac{Ax + B}{ax^2 + bx + c} + \frac{Cx + D}{(ax^2 + bx + c)^2} + \dots + \frac{Ex + F}{(ax^2 + bx + c)^n} $$
Veamos ahora cómo se aplica este procedimiento en distintos casos concretos.
A] Denominador con raíces reales simples
Consideremos la integral $$ \int \frac{x - 1}{x^2 + 3x} \ dx $$
El grado del numerador es menor que el del denominador, por lo que no es necesario realizar ninguna división previa.
Factorizamos el denominador:
$$ \int \frac{x - 1}{x(x + 3)} \ dx $$
Las raíces \( x = 0 \) y \( x = -3 \) son simples. Por tanto, podemos escribir:
$$ \int \frac{x - 1}{x(x + 3)} \ dx = \int \left( \frac{A}{x} + \frac{B}{x + 3} \right) dx $$
Unificando denominadores:
$$ = \int \frac{A(x + 3) + Bx}{x(x + 3)} \ dx $$
Al simplificar el numerador se obtiene:
$$ = \int \frac{(A + B)x + 3A}{x(x + 3)} \ dx $$
Igualando coeficientes con el numerador original \( x - 1 \), se obtiene el sistema:
$$ \begin{cases} A + B = 1 \\ 3A = -1 \end{cases} $$
De aquí se deduce \( A = -\frac{1}{3} \) y \( B = \frac{4}{3} \).
Sustituyendo:
$$ \int \frac{x - 1}{x(x + 3)} \ dx = \int \left( -\frac{1}{3x} + \frac{4}{3(x + 3)} \right) dx $$
Aplicando la linealidad de la integral:
$$ = -\frac{1}{3} \int \frac{1}{x} \ dx + \frac{4}{3} \int \frac{1}{x + 3} \ dx $$
Ambas integrales son elementales:
$$ \int \frac{1}{x} \ dx = \log|x| + C, \qquad \int \frac{1}{x + 3} \ dx = \log|x + 3| + C $$
Por tanto, el resultado final es:
$$ \int \frac{x - 1}{x(x + 3)} \ dx = -\frac{1}{3} \log|x| + \frac{4}{3} \log|x + 3| + C $$
B] Denominador con una raíz de multiplicidad 2
Consideremos ahora la integral
$$ \int \frac{2x+5}{(x+1)(x+3)^2} \ dx $$
El denominador tiene dos raíces reales: \( x = -1 \), simple, y \( x = -3 \), con multiplicidad 2.
La descomposición en fracciones parciales es entonces:
$$ \int \frac{2x+5}{(x+1)(x+3)^2} \ dx = \int \left( \frac{A}{x+1} + \frac{B}{x+3} + \frac{C}{(x+3)^2} \right) dx $$
Unificando denominadores:
$$ = \int \frac{A(x+3)^2 + B(x+1)(x+3) + C(x+1)}{(x+1)(x+3)^2} \ dx $$
Desarrollando y agrupando términos:
$$ = \int \frac{(A + B)x^2 + (6A + 4B + C)x + (9A + 3B + C)}{(x+1)(x+3)^2} \ dx $$
Al igualar con el numerador original \( 2x + 5 \), se obtiene el sistema:
Explicación. Comparación de coeficientes: • \( A + B = 0 \) • \( 6A + 4B + C = 2 \) • \( 9A + 3B + C = 5 \)
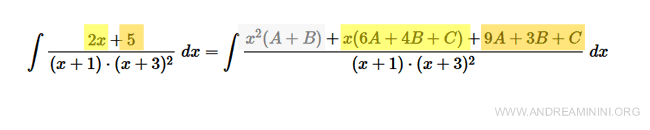
La solución del sistema es:
$$ B = -\frac{3}{4}, \quad A = \frac{3}{4}, \quad C = \frac{1}{2} $$
Sustituyendo:
$$ \int \frac{2x+5}{(x+1)(x+3)^2} \ dx = \int \left( \frac{3}{4(x+1)} - \frac{3}{4(x+3)} + \frac{1}{2(x+3)^2} \right) dx $$
Integrando término a término:
$$ = \frac{3}{4} \log|x+1| - \frac{3}{4} \log|x+3| - \frac{1}{2(x+3)} + C $$
Nota. Dado que $$ \frac{d}{dx}[-(x+3)^{-1}] = \frac{1}{(x+3)^2}, $$ se tiene $$ \int \frac{1}{(x+3)^2} \ dx = -\frac{1}{x+3}. $$
C] Denominador con raíces complejas
Por último, consideremos la integral
$$ \int \frac{x-1}{x(x^2+1)} \ dx $$
El denominador contiene una raíz real \( x = 0 \) y un factor cuadrático irreducible \( x^2 + 1 \).
La descomposición adecuada es:
$$ \int \frac{x-1}{x(x^2+1)} \ dx = \int \left( \frac{A}{x} + \frac{Bx+C}{x^2+1} \right) dx $$
Al unificar denominadores y comparar coeficientes se obtiene:
$$ A = -1, \quad B = 1, \quad C = 1 $$
Sustituyendo:
$$ \int \frac{x-1}{x(x^2+1)} \ dx = \int \left( -\frac{1}{x} + \frac{x+1}{x^2+1} \right) dx $$
Separando términos:
$$ = - \int \frac{1}{x} \ dx + \int \frac{x}{x^2+1} \ dx + \int \frac{1}{x^2+1} \ dx $$
Las integrales resultantes son bien conocidas:
- $$ \int \frac{1}{x} \ dx = \log|x| + C $$
- $$ \int \frac{x}{x^2+1} \ dx = \frac{1}{2} \log(x^2+1) $$
- $$ \int \frac{1}{x^2+1} \ dx = \arctan(x) $$
Por tanto, el resultado final es:
$$ \int \frac{x-1}{x(x^2+1)} \ dx = -\log|x| + \frac{1}{2} \log(x^2+1) + \arctan(x) + C $$
Con esto se completa la integración mediante fracciones parciales.