Każdy podzbiór spójny zawiera się w dokładnie jednej składowej spójnej przestrzeni

Niech $ A $ i $ B $ będą podzbiorami przestrzeni topologicznej $ X $. Zakładamy, że zbiór $ A $ jest spójny oraz że $ A \subset B $. Jeżeli zbiór $ B $ dopuszcza w przestrzeni $ X $ rozdział na dwa podzbiory $ B_1 $ i $ B_2 $, wówczas zbiór $ A $ musi w całości zawierać się w jednym z nich: $$ A \subset B_1 \quad \text{lub} \quad A \subset B_2 $$

Innymi słowy, zbiór spójny nie może jednocześnie przecinać obu części rozdziału.

Jeżeli zbiór spójny jest zawarty w zbiorze, który rozpada się na dwie rozłączne części, nie może on zostać pomiędzy nie rozdzielony. Musi w całości należeć do jednej z nich.

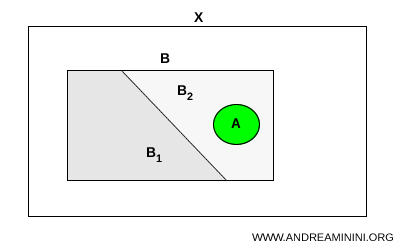
podzbiór spójny zawarty w jednej składowej spójnej przestrzeni topologicznej

Sens tego twierdzenia można łatwo uchwycić dzięki intuicyjnej analogii. Wyobraźmy sobie zbiór spójny jako nieprzerwaną linę umieszczoną wewnątrz pewnej obudowy. Jeżeli obudowa zostaje podzielona na dwa rozłączne przedziały, a lina pozostaje ciągła, nie może ona jednocześnie znaleźć się w obu częściach. Aby tak się stało, musiałaby zostać przerwana. Właśnie tę zasadniczą niemożność „przecięcia" zbioru przez rozdział formalizuje pojęcie spójności.

Przykład
Dowód

Przykład

Rozważmy klasyczny przykład z przestrzeni liczb rzeczywistych:

$$ X = \mathbb{R} $$

oraz jej podzbiór:

$$ B = (-3,4) $$

Zbiór ten można w naturalny sposób rozdzielić na dwa podzbiory:

$$ B_1 = (-3,0) $$

$$ B_2 = (0,4) $$

Zbiory te są rozłączne:

$$ B_1 \cap B_2 = \varnothing $$

a ich suma odtwarza dokładnie zbiór wyjściowy:

$$ B_1 \cup B_2 = B $$

Ponadto zbiory $ B_1 $ i $ B_2 $ są otwarte w topologii podprzestrzeni indukowanej na $ B $.

W konsekwencji rzeczywiście stanowią one rozdział zbioru $ B $ w przestrzeni $ X $.

Rozważmy teraz podzbiór spójny zbioru $ B $:

$$ A = (1,2) $$

Łatwo zauważyć, że $ A \subset B_2 $. Zbiór $ A $ zawiera się więc w całości w jednej z dwóch części rozdziału, dokładnie tak, jak przewiduje to ogólne twierdzenie.

Uwaga. Jeżeli natomiast rozważymy $ A = (-1,1) $, otrzymamy $$ A \cap B_1 \neq \varnothing, \qquad A \cap B_2 \neq \varnothing $$ Taka sytuacja nie może jednak wystąpić, ponieważ $ B_1 $ i $ B_2 $ tworzą rozdział zbioru $ B $. Zbiór spójny nie może być rozłożony pomiędzy obie części rozdziału. Gdyby było inaczej, sam zbiór $ A $ admitowałby rozdział, co pozostawałoby w sprzeczności z podstawowym faktem, że przedział $ (-1,1) $ jest zbiorem spójnym. Kluczowy jest tu nie brak spójności przedziału $ (-1,1) $, lecz niemożność jego zawarcia w zbiorze rozdzielonym w taki sposób.

Dowód

Założenia

Niech $ A $ i $ B $ będą podzbiorami przestrzeni topologicznej $ X $.

$$ A \subset X \quad \text{i} \quad B \subset X $$

Zakładamy, że:

$ A $ jest zbiorem spójnym
$ A \subset B $
$ B_1 $ i $ B_2 $ tworzą rozdział zbioru $ B $ w przestrzeni $ X $

Teza

Przy powyższych założeniach zbiór $ A $ zawiera się w $ B_1 $ lub w $ B_2 $:

$$ A \subset B_1 \quad \text{lub} \quad A \subset B_2 $$

Dowód

Z założenia $ B_1 $ i $ B_2 $ stanowią rozdział zbioru $ B $ w przestrzeni $ X $. W szczególności spełnione są następujące warunki:

$ B_1 \cap B_2 = \varnothing $
$ B = B_1 \cup B_2 $
$ B_1 $ i $ B_2 $ są zbiorami otwartymi w topologii podprzestrzeni indukowanej na $ B $

Przypuśćmy, w celu uzyskania sprzeczności, że zbiór $ A $ nie zawiera się w całości ani w $ B_1 $, ani w $ B_2 $. Wówczas:

$$ A \cap B_1 \neq \varnothing \qquad \text{i} \qquad A \cap B_2 \neq \varnothing $$

Ponieważ $ A \subset B $, możemy zapisać:

$$ A = A \cap B = A \cap (B_1 \cup B_2) = (A \cap B_1) \cup (A \cap B_2) $$

Zbiory $ A \cap B_1 $ oraz $ A \cap B_2 $ są rozłączne, gdyż rozłączne są zbiory $ B_1 $ i $ B_2 $.

Ponadto, ponieważ $ B_1 $ i $ B_2 $ są otwarte w $ B $, zbiory $ A \cap B_1 $ oraz $ A \cap B_2 $ są otwarte w topologii podprzestrzeni indukowanej na $ A $.

Otrzymujemy w ten sposób dwa rozłączne, niepuste i otwarte podzbiory zbioru $ A $, które wyznaczają jego rozdział.

Pozostaje to w sprzeczności z założeniem, że $ A $ jest zbiorem spójnym.

Wnioskujemy stąd, że początkowe przypuszczenie było fałszywe, a zatem:

$$ A \subset B_1 \quad \text{lub} \quad A \subset B_2 $$

Teza została tym samym udowodniona.

I tak dalej.