Przestrzenie po prostu spójne w topologii

Przestrzeń topologiczną nazywamy po prostu spójną, jeśli każdą zamkniętą krzywą w tej przestrzeni można w sposób ciągły skurczyć do jednego punktu, nie wychodząc poza nią.

Inaczej mówiąc, przestrzeń jest po prostu spójna, gdy każdą pętlę można płynnie „ściągnąć" do punktu, pozostając cały czas w jej wnętrzu. Oznacza to, że taka przestrzeń stanowi spójną, nieprzerwaną całość - bez wewnętrznych dziur czy pustych obszarów.

Uwaga: każda przestrzeń po prostu spójna jest zarazem spójna, lecz nie każda przestrzeń spójna jest po prostu spójna. Prosta spójność to silniejsze wymaganie.

Przykład: sfera i torus

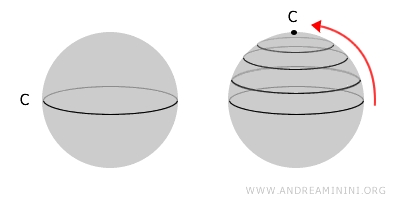
Sfera jest klasycznym przykładem przestrzeni po prostu spójnej. Każdą zamkniętą krzywą narysowaną na jej powierzchni można stopniowo zwinąć do jednego punktu, nie naruszając powierzchni sfery.

Dla kontrastu, torus - czyli kształt przypominający pączek - nie jest po prostu spójny. Jego środkowy otwór uniemożliwia „ściągnięcie" pewnych pętli do punktu, ponieważ każda taka próba wymagałaby przejścia przez pustą przestrzeń w środku torusa.

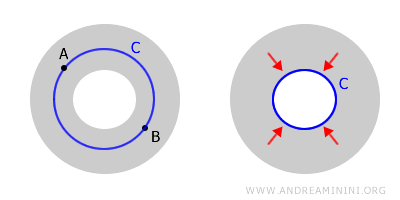
Oba przykłady dobrze pokazują różnicę między spójnością a prostą spójnością. Torus pozostaje przestrzenią spójną - dowolne dwa punkty można połączyć ścieżką przebiegającą całkowicie wewnątrz niego - ale nie jest po prostu spójny, ponieważ nie każdą pętlę da się zredukować do punktu.

Przestrzenie, które są spójne, lecz nie po prostu spójne, określa się mianem wielokrotnie spójnych. Typowymi przykładami są pierścień oraz przestrzeń toroidalna.

Podsumowując, prosta spójność to bardziej restrykcyjny warunek niż zwykła spójność łukowa - opisuje przestrzenie całkowicie pozbawione „dziur", w których każdą pętlę można gładko zwinąć do jednego punktu.