Spójność wynikająca ze wspólnej części

Niech \( C_1, C_2, \dots, C_n \subset X \) będą zbiorami spójnymi przestrzeni topologicznej \( X \), takimi że ich część wspólna nie jest pusta: \[
\bigcap_{i=1}^n C_i \neq \varnothing . \] Wówczas ich suma mnogościowa \( \bigcup_{i=1}^n C_i \) również jest zbiorem spójnym.

Mówiąc prościej: jeżeli kilka zbiorów spójnych ma choć jeden punkt wspólny, to ich połączenie również pozostaje spójne.

Wynik ten opiera się na fundamentalnej własności spójności. Obecność punktu wspólnego uniemożliwia bowiem rozdzielenie całości na dwie rozłączne, niepuste części otwarte.

Uwaga. Warunek \( \bigcap_{i=1}^n C_i \neq \varnothing \) jest wystarczający do zapewnienia spójności sumy \( \bigcup_{i=1}^n C_i \), lecz nie jest warunkiem koniecznym. Suma zbiorów spójnych może pozostać spójna również wtedy, gdy nie istnieje jeden punkt wspólny dla wszystkich zbiorów. Dzieje się tak na przykład wtedy, gdy zbiory nachodzą na siebie stopniowo, tworząc tzw. łańcuch połączeń.

Przykład

Rozważmy następujące podzbiory przestrzeni \( \mathbb{R}^2 \):

• \( C_1 \): odcinek poziomy łączący punkty \( (-1,0) \) oraz \( (1,0) \),
• \( C_2 \): odcinek pionowy łączący punkty \( (0,-1) \) oraz \( (0,1) \),
• \( C_3 \): odcinek ukośny łączący punkty \( (-1,-1) \) oraz \( (1,1) \).

Każdy z tych zbiorów jest spójny.

Co więcej, wszystkie trzy mają punkt wspólny, a mianowicie \( (0,0) \). Rzeczywiście:

\[ (0,0) \in C_1 \cap C_2 \cap C_3 \]

Stąd wynika, że ich część wspólna nie jest pusta:

\[ \bigcap_{i=1}^3 C_i = \{(0,0)\} \]

Zgodnie z omówionym kryterium ich suma jest więc zbiorem spójnym:

\[ C_1 \cup C_2 \cup C_3 \]

Trzy odcinki przecinają się w jednym punkcie, co zapewnia spójność całej figury.

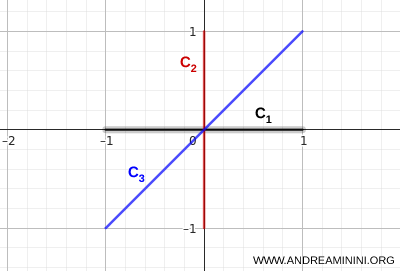
Z dowolnego punktu jednego z odcinków można dotrzeć do dowolnego innego, poruszając się wyłącznie w obrębie ich sumy.

Uwaga. Istnieją również inne kryteria spójności, które nie wymagają istnienia jednego punktu wspólnego dla wszystkich zbiorów. Na przykład, jeżeli zbiory \( C_i \) są spójne i spełniają warunek \( C_i \cap C_{i+1} \neq \varnothing \), to ich suma \( \bigcup_i C_i \) jest spójna, nawet gdy \( \bigcap_i C_i = \varnothing \). Warunek ten nie jest jednak konieczny. Suma może pozostać spójna także wtedy, gdy niektóre kolejne pary zbiorów są rozłączne, o ile inne zapewniają ciągłość połączenia. Klasycznym przykładem są trzy odcinki tworzące trójkąt. Pomimo że ich część wspólna jest pusta, czyli \( \bigcap_i C_i = \varnothing \), ich suma pozostaje spójna.

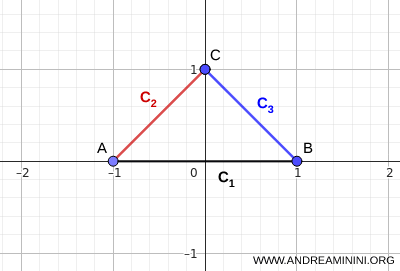
Ten przykład jasno pokazuje, że spójność może wynikać z lokalnych połączeń między zbiorami.

Dowód

Niech \( X \) będzie przestrzenią topologiczną, a \( \{C_i\}_{i \in I} \) rodziną zbiorów spójnych w \( X \), takich że

\[ \bigcap_{i \in I} C_i \neq \varnothing . \]

Przypuśćmy nie wprost, że suma

\[ C = \bigcup_{i \in I} C_i \]

nie jest zbiorem spójnym.

Wówczas istnieją zbiory otwarte \( U \) oraz \( V \), które tworzą rozkład zbioru \( C \), to znaczy:

• \( U \cap C \neq \varnothing \),
• \( V \cap C \neq \varnothing \),
• \( (U \cap C) \cap (V \cap C) = \varnothing \),
• \( C = (U \cap C) \cup (V \cap C) \).

Ponieważ część wspólna zbiorów \( C_i \) nie jest pusta, istnieje punkt

\[ x \in \bigcap_{i \in I} C_i .\]

Punkt ten należy do wszystkich zbiorów \( C_i \), a więc także do \( C \). Musi on zatem należeć do jednego z rozłącznych zbiorów \( U \) lub \( V \), lecz nie do obu jednocześnie. Bez straty ogólności załóżmy, że

\[ x \in U \quad \text{oraz} \quad x \notin V .\]

Ponieważ każdy zbiór \( C_i \) jest podzbiorem \( C \), zachodzi:

\[ C_i = (C_i \cap U) \cup (C_i \cap V). \]

Zbiory \( C_i \cap U \) oraz \( C_i \cap V \) są otwarte w topologii indukowanej na \( C_i \), są rozłączne i ich suma daje cały zbiór \( C_i \). Ponieważ jednak każdy \( C_i \) jest spójny, jeden z tych zbiorów musi być pusty.

Wynika stąd, że każdy zbiór \( C_i \) zawiera się w całości albo w \( U \), albo w \( V \).

Ponieważ \( x \in C_i \) oraz \( x \in U \), nie może zachodzić \( C_i \subset V \). Otrzymujemy więc:

\[ C_i \subset U \quad \text{dla każdego } i \in I .\]

W konsekwencji cała suma spełnia:

\[ \bigcup_{i \in I} C_i \subset U .\]

Pozostaje to w sprzeczności z założeniem, że \( V \cap C \neq \varnothing \).

Sprzeczność ta dowodzi, że początkowe założenie było fałszywe. W rezultacie suma \( \bigcup_{i \in I} C_i \) jest zbiorem spójnym.

Na tym kończy się dowód.