Twierdzenie: jak rozpoznać przestrzeń spójną dzięki zbiorom otwartym i domkniętym
Przestrzeń topologiczną \( X \) nazywamy spójną, jeśli i tylko jeśli jedynymi jej podzbiorami, które są jednocześnie otwarte i domknięte (czyli clopen), są cała przestrzeń \( X \) oraz zbiór pusty \( \emptyset \).
W prostszych słowach: przestrzeń jest spójna, gdy nie da się jej rozdzielić na dwa rozłączne i niepuste zbiory otwarte. W takiej sytuacji jedynymi zbiorami clopen pozostają dwa oczywiste przypadki - cała przestrzeń i zbiór pusty.
To twierdzenie jest jednym z najważniejszych narzędzi w topologii. Umożliwia stwierdzenie spójności przestrzeni bez sięgania po bardziej złożone pojęcia, takie jak spójność łukowa.
Jak to rozumieć
W topologii podzbiór, który jest jednocześnie otwarty i domknięty, rozdziela przestrzeń. Oznacza to, że dzieli \( X \) na dwa rozłączne, niepuste zbiory otwarte.
Jeśli taki zbiór istnieje, przestrzeń można przedstawić jako sumę dwóch rozłącznych zbiorów otwartych, a więc nie jest ona spójna (w literaturze używa się też określenia rozłączna).
Natomiast jeśli jedynymi zbiorami clopen w \( X \) są \( X \) i \( \emptyset \), to żadne topologiczne rozdzielenie przestrzeni nie jest możliwe. Wtedy \( X \) jest spójna.
Uwaga: w każdej przestrzeni topologicznej zarówno cała przestrzeń \( X \), jak i zbiór pusty \( \emptyset \) są zawsze jednocześnie otwarte i domknięte. To dwa trywialne, ale ważne przypadki zbiorów clopen.
Przykład 1: skończona przestrzeń niespójna
Rozważmy \( X = \{ a, b, c, d \} \) z topologią \( T \), w której zbiorami otwartymi są \( \{ b \}, \{ a, b \}, \{ c, d \}, \{ b, c, d \}, \{ a, b, c, d \} \) oraz \( \emptyset \).
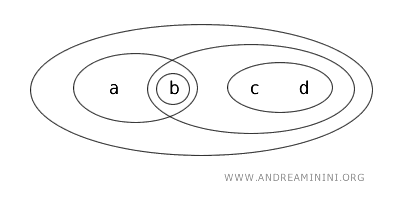
W tej przestrzeni podzbiór \( \{ a, b \} \) jest clopen, ponieważ:
- jest otwarty, gdyż należy do rodziny zbiorów otwartych topologii \( T \);
- jest też domknięty, ponieważ jego dopełnienie \( X \setminus \{ a, b \} = \{ c, d \} \) również jest otwarte w \( T \).
Zatem przestrzeń topologiczna \( (X, T) \) jest niespójna, bo zawiera właściwy, niepusty zbiór, który jest clopen.
Już jeden taki przypadek wystarczy, aby uznać przestrzeń za niespójną. Oznacza to, że można ją rozłożyć na dwa niepuste, rozłączne zbiory otwarte: \( \{ a, b \} \) oraz \( \{ c, d \} \). Tym samym nie spełnia ona warunku spójności topologicznej.
Przykład 2: prosta rzeczywista
Weźmy przestrzeń \( \mathbb{R} \) z topologią standardową, generowaną przez wszystkie przedziały otwarte \( (a, b) \).
W tej topologii przedziały \( (a, b) \) są otwarte, ale nie są domknięte, natomiast przedziały \( [a, b] \) są domknięte, lecz nie otwarte.
Jedynymi zbiorami, które są jednocześnie otwarte i domknięte w \( \mathbb{R} \), są \( \mathbb{R} \) i \( \emptyset \).
Dlatego prosta rzeczywista z topologią standardową jest spójną przestrzenią topologiczną.
Przykład 3: niespójna podprzestrzeń prostej rzeczywistej
Rozważmy podzbiór \( X = (0,1) \cup (2,3) \subset \mathbb{R} \) z topologią podprzestrzeni, czyli topologią odziedziczoną po standardowej topologii na \( \mathbb{R} \).
W tej topologii oba przedziały, \( (0,1) \) i \( (2,3) \), są jednocześnie otwarte i domknięte w \( X \), ponieważ dopełnienie każdego z nich w \( X \) jest drugim przedziałem. Dokładniej:
- dopełnieniem \( (0,1) \) w \( X \) jest \( (2,3) \), które jest otwarte w \( X \);
- dopełnieniem \( (2,3) \) w \( X \) jest \( (0,1) \), również otwarte w \( X \).
Oba te zbiory są więc clopen.
Skoro w \( X \) istnieją nietrywialne zbiory będące jednocześnie otwartymi i domkniętymi, oznacza to, że przestrzeń \( X \) jest niespójna.
Innymi słowy, \( X \) składa się z dwóch składowych spójnych: \( (0,1) \) oraz \( (2,3) \). Są to dwa rozłączne, niepuste otwarte podzbiory, których punktów nie da się połączyć ciągłą krzywą. Właśnie ta niemożność „połączenia” ich w sensie topologicznym stanowi o braku spójności przestrzeni.