Zbiory clopen
Zbiór nazywamy clopen, jeśli w danej topologii jest jednocześnie otwarty i domknięty.
Tego rodzaju zbiory są interesujące, ponieważ wymykają się potocznemu wyobrażeniu o topologii. Na pierwszy rzut oka może się wydawać, że zbiór nie powinien być jednocześnie otwarty i domknięty, a jednak w wielu przestrzeniach jest to możliwe i prowadzi do ciekawych konsekwencji teoretycznych.
Określenie „clopen” powstało z połączenia angielskich słów „closed” i „open”. Podkreśla to ich podwójny charakter: łączą własności typowe dla zbiorów otwartych i zbiorów domkniętych.
Zbiór jest clopen wtedy i tylko wtedy, gdy on sam oraz jego dopełnienie są otwarte w tej samej topologii.
Uwaga : W klasycznej topologii na zbiorze liczb rzeczywistych zbiory clopen są rzadkością. Pojawiają się jednak naturalnie w wielu innych przestrzeniach i często pozwalają lepiej zrozumieć ich strukturę, pełniąc ważną funkcję w analizie topologicznej.
Przykład
Rozważmy zbiór \(X=\{a,b,c,d\}\) wraz z topologią \(T\).
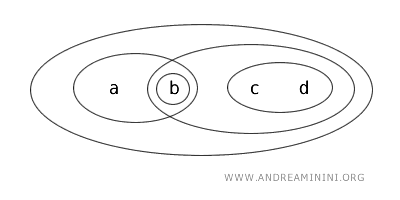
Załóżmy, że zbiorami otwartymi w \(T\) są: \(\{b\}, \{a,b\}, \{c,d\}, \{b,c,d\}, \{a,b,c,d\}, \varnothing\).
W takim układzie podzbiór \(\{a,b\}\) jest zbiorem otwartym.
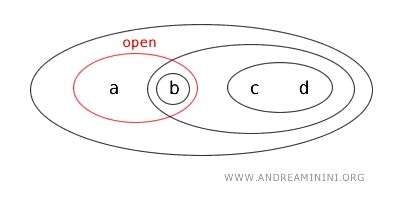
Jednocześnie jest on dopełnieniem zbioru \(\{c,d\}\) w \(X\):
$$ X - \{ c,d \} = \{a , b \} $$
A ponieważ dopełnienie zbioru otwartego jest zawsze zbiorem domkniętym, otrzymujemy:
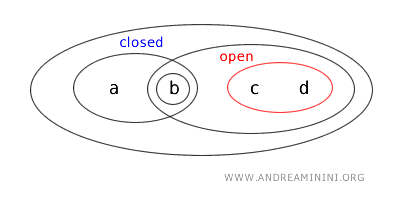
Tym samym \(\{a,b\}\) jest jednocześnie otwarty i domknięty, czyli jest zbiorem clopen.
Zbiór pusty i zbiór całkowity
W każdej topologii na zbiorze \(X\) zarówno zbiór pusty \((\varnothing)\), jak i zbiór całkowity \((X)\) są zawsze clopen.
Wynika to bezpośrednio z definicji zbiorów otwartych i domkniętych. Z aksjomatów topologii wiemy, że \(\varnothing\) i \(X\) są zawsze otwarte. Z kolei zbiór jest domknięty wtedy i tylko wtedy, gdy jego dopełnienie jest otwarte.
- Zbiór pusty (\(\varnothing\))
Jest otwarty z definicji. Jest również domknięty, ponieważ jego dopełnienie \(X \setminus \varnothing = X\) jest otwarte. Zatem \(\varnothing\) jest clopen. - Zbiór całkowity (\(X\))
Jest otwarty z definicji i równocześnie domknięty, gdyż \(X \setminus X = \varnothing\) jest otwarte. Z tego powodu \(X\) także jest clopen.
Te dwa przypadki są pierwszymi i najbardziej podstawowymi przykładami zbiorów clopen, pojawiającymi się w każdej topologii.
W innych przestrzeniach zbiory tego typu mogą ujawniać znacznie głębsze własności, dlatego pojęcie clopen stanowi użyteczne narzędzie w analizie topologicznej.