Brzeg zbioru

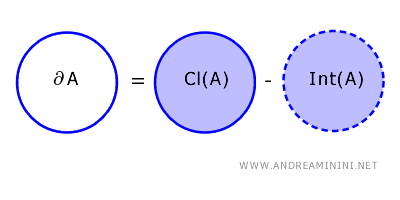
Brzeg podzbioru \( A \) przestrzeni topologicznej \( X \) to zbiór punktów, które należą do domknięcia \( A \), ale nie należą do jego wnętrza : \[ \partial A = \text{Cl}(A) - \text{Int}(A) \]

Oznaczenie \( \text{Cl}(A) \) odnosi się do domknięcia zbioru \( A \), czyli zbioru zawierającego zarówno punkty samego \( A \), jak i wszystkie jego punkty skupienia.

Z kolei \( \text{Int}(A) \) oznacza wnętrze zbioru \( A \), rozumiane jako zbiór punktów, dla których istnieje pewne otoczenie w całości zawarte w \( A \).

Istotne jest, że pojęcie brzegu nie jest własnością samego zbioru w sensie absolutnym, lecz zależy od topologii, jaką rozważamy na danej przestrzeni.

Oznacza to, że ten sam zbiór może mieć różny brzeg w zależności od przyjętej struktury topologicznej.

Można więc powiedzieć, że brzeg zbioru \( A \) tworzą te punkty, które są jednocześnie „blisko" zbioru \( A \) oraz jego dopełnienia \( X \setminus A \).

Przykład konkretny

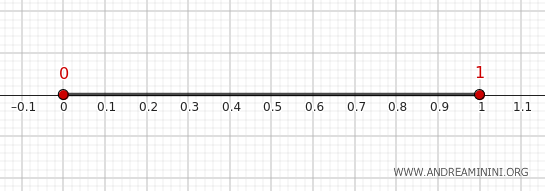
Rozważmy zbiór \( A = (0, 1) \), traktowany jako podzbiór prostej rzeczywistej \( \mathbb{R} \), wyposażonej w jej standardową topologię.

Wyznaczmy jego brzeg, analizując kolejno odpowiednie pojęcia.

1] Domknięcie zbioru A

Domknięcie zbioru \( A \), oznaczane przez \( \text{Cl}(A) \), obejmuje wszystkie punkty należące do \( A \) oraz jego punkty skupienia.

W przypadku zbioru \( A = (0, 1) \) domknięciem jest przedział domknięty \([0, 1]\), ponieważ zarówno 0, jak i 1 są punktami granicznymi tego zbioru, podobnie jak wszystkie punkty leżące pomiędzy nimi.

$$ \text{Cl}(A) = [0, 1] $$

2] Wnętrze zbioru A

Wnętrze zbioru \( A \), oznaczane przez \( \text{Int}(A) \), składa się z punktów, które posiadają otoczenie całkowicie zawarte w \( A \).

Ponieważ \( A = (0, 1) \) jest zbiorem otwartym, jego wnętrze pokrywa się z nim samym:

$$ \text{Int}(A) = (0, 1) $$

3] Brzeg zbioru A

Brzeg zbioru \( A \), czyli \( \partial A \), otrzymujemy, odejmując jego wnętrze od domknięcia:

$$ \partial A = \text{Cl}(A) - \text{Int}(A) $$

Po podstawieniu wcześniej wyznaczonych zbiorów otrzymujemy:

$$ \partial A = [0, 1] - (0, 1) = \{0, 1\} $$

Zatem w topologii standardowej prostej \( \mathbb{R} \) brzeg zbioru \( A = (0,1) \) stanowią punkty \(\{0, 1\}\).

Są to punkty leżące „na granicy" zbioru, ponieważ każde ich otoczenie zawiera jednocześnie elementy zbioru \( A \) oraz jego dopełnienia \( X \setminus A \).

Twierdzenie o brzegu zbioru

Punkt \( x \in X \) należy do brzegu \( \partial A \) podzbioru \( A \) wtedy i tylko wtedy, gdy każde otoczenie punktu \( x \) ma część wspólną zarówno ze zbiorem \( A \), jak i z jego dopełnieniem \( X - A \).

Twierdzenie to daje praktyczne i intuicyjne kryterium: aby sprawdzić, czy punkt \( x \) leży na brzegu zbioru \( A \), wystarczy upewnić się, że każde jego otoczenie przecina jednocześnie zbiór \( A \) oraz zbiór \( X - A \).

Przykład

Rozpatrzmy ponownie zbiór \( A = (0, 1) \) w przestrzeni \( \mathbb{R} \), wyposażonej w topologię standardową.

W tym przypadku otrzymujemy:

$$ \text{Cl}(A) = [0, 1] \quad \text{oraz} \quad \text{Int}(A) = (0, 1) $$

Stąd bezpośrednio wynika, że brzeg zbioru ma postać:

$$ \partial A = \{0, 1\} $$

Sprawdźmy teraz krok po kroku, że punkty te spełniają kryterium zawarte w twierdzeniu o brzegu.

1] Sprawdzenie dla punktu 0

Rozważmy dowolne otoczenie punktu 0, na przykład przedział \( (0 - \epsilon, 0 + \epsilon) \), gdzie \( \epsilon > 0 \).

Takie otoczenie przecina zbiór \( A \), ponieważ zawiera punkty należące do przedziału \( (0, 1) \). Jednocześnie przecina ono zbiór \( X - A \), gdyż obejmuje również punkty mniejsze lub równe 0.

Oznacza to, że punkt 0 spełnia warunek brzegowy, a więc \( 0 \in \partial A \).

 

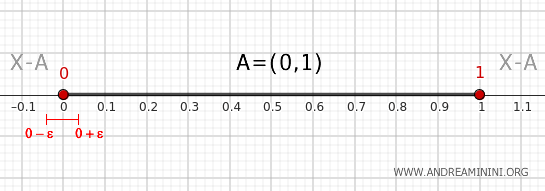
2] Sprawdzenie dla punktu 1

Analogicznie rozważmy otoczenie punktu 1, na przykład przedział \( (1 - \epsilon, 1 + \epsilon) \).

Takie otoczenie również przecina zbiór \( A \), ponieważ zawiera punkty z przedziału \( (0,1) \), a jednocześnie przecina zbiór \( X - A \), gdyż zawiera punkty większe lub równe 1.

W rezultacie także punkt 1 należy do brzegu zbioru, czyli \( 1 \in \partial A \).

3] Sprawdzenie dla punktu wewnętrznego

Wybierzmy teraz dowolny punkt wewnętrzny zbioru \( A \), na przykład 0,5.

Każde otoczenie punktu 0,5 jest w całości zawarte w zbiorze \( A \) i w związku z tym nie może przecinać jego dopełnienia \( X - A \).

Z tego wynika, że punkt 0,5 nie spełnia warunku brzegowego, a więc \( 0.5 \notin \partial A \).

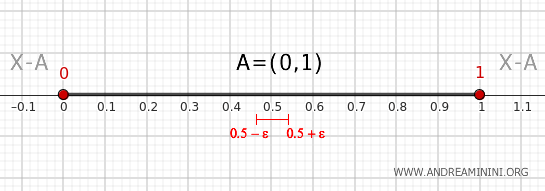
Podsumowując, twierdzenie jednoznacznie potwierdza, że punkty 0 i 1 należą do brzegu zbioru \( A = (0, 1) \), natomiast punkt taki jak 0,5 do brzegu nie należy. Brzeg tego zbioru jest więc równy \(\{0, 1\}\).

Uwagi

Poniżej przedstawiono kilka istotnych własności brzegów zbiorów, które często pojawiają się w topologii:

• Brzeg \( \partial A \) jest zawarty w \( A \) wtedy i tylko wtedy, gdy \( A \) jest zbiorem domkniętym:
  \[ \partial A \subseteq A \Leftrightarrow A \text{ jest domknięty} \]
• Brzeg \( \partial A \) i zbiór \( A \) są rozłączne wtedy i tylko wtedy, gdy \( A \) jest zbiorem otwartym:
  Innymi słowy, zbiór \( A \) jest otwarty wtedy i tylko wtedy, gdy żaden z jego punktów nie leży na jego brzegu.
  \[ \partial A \cap A = \emptyset \Leftrightarrow A \text{ jest otwarty} \]
• Brzeg \( \partial A \) jest pusty wtedy i tylko wtedy, gdy \( A \) jest jednocześnie zbiorem otwartym i domkniętym (clopen):
  \[ \partial A = \emptyset \Leftrightarrow A \text{ jest clopen} \]
• Brzeg \( \partial A \) jest częścią wspólną domknięcia zbioru \( A \) oraz domknięcia jego dopełnienia \( X - A \):
  \[ \partial A = \text{Cl}(A) \cap \text{Cl}(X - A) \]
• Brzeg \( \partial A \) jest zawsze zbiorem domkniętym:
  

  Część wspólna dwóch zbiorów domkniętych jest również zbiorem domkniętym. Ponieważ \( \partial A \) jest określony jako \(\text{Cl}(A) \cap \text{Cl}(X - A)\), wynika stąd, że brzeg zbioru jest zawsze domknięty.

• Brzeg zbioru i jego wnętrze są zawsze rozłączne:
  \[ \partial A \cap \text{Int}(A) = \emptyset \]
• Suma wnętrza zbioru i jego brzegu jest równa domknięciu zbioru:
  \[ \partial A \cup \text{Int}(A) = \text{Cl}(A) \]

I tak dalej.