Topologia zbiorów otwartych
Topologia T na zbiorze X to wybrana rodzina jego podzbiorów, które uznajemy za zbiory „otwarte”. Aby taka rodzina mogła zostać nazwana topologią, musi spełniać dwa podstawowe warunki:
- zarówno zbiór pusty ∅, jak i cały zbiór X muszą być otwarte,
- suma oraz przecięcie skończonej liczby zbiorów otwartych również muszą być zbiorami otwartymi.
Innymi słowy, topologia T może zawierać wyłącznie podzbiory zbioru X i musi być domknięta na operacje sum oraz przecięć. Jest to podstawowy warunek, który pozwala nam na logiczne i spójne definiowanie pojęcia „zbioru otwartego” w ujęciu abstrakcyjnym.
Kiedy mówimy o kolekcji zbiorów, mamy na myśli zbiór, którego elementami są inne zbiory lub ich podzbiory. W topologii taka kolekcja pełni kluczową rolę, ponieważ określa strukturę przestrzeni, z którą pracujemy.
Para (X,T) nosi nazwę przestrzeni topologicznej. To właśnie w takiej przestrzeni możemy badać ciągłość, zbieżność, granice czy własności funkcji - wszystko bez konieczności odwoływania się do konkretnej geometrii lub metryki.
Uwaga: dla wygody często mówi się po prostu, że „X jest przestrzenią topologiczną”. W rzeczywistości jednak przestrzeń topologiczna to zawsze para (X,T): zbiór X oraz topologia T, która określa, jakie jego podzbiory uznajemy za otwarte.
Dlaczego zbiór pusty jest otwarty?
Przyjmuje się to jako zasadę. Włączenie zbioru pustego do każdej topologii zapewnia spójność wszystkich dalszych definicji i twierdzeń.
Przykład
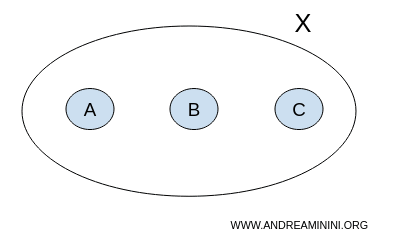
Weźmy prosty zbiór:
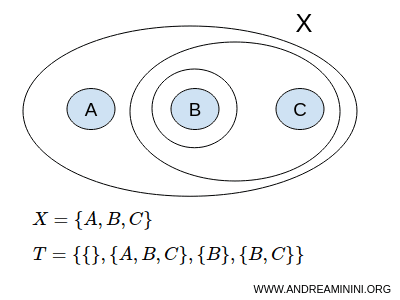
$$ X = \{ A,B,C \} $$
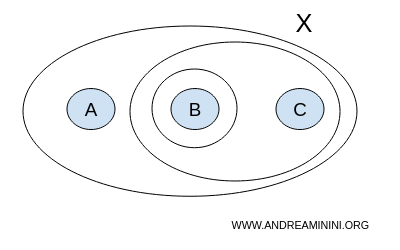
Jedna z możliwych topologii T na tym zbiorze może wyglądać następująco:
$$ T = \{ \{ \},\{A,B,C\}, \{B\}, \{B,C\} \} $$
Zbiór { } oznacza zbiór pusty, a {A,B,C} to cały zbiór X, czyli podzbiór niewłaściwy.
Zauważmy teraz, że suma dowolnych zbiorów z T znów należy do T:
$$ \{ B \} \cup \{ B, C \} \subseteq \{ B, C \} \subseteq T$$
$$ \{ B \} \cup \{ A, B, C \} \subseteq \{ A, B, C \} \subseteq T$$
$$ \{ B \} \cup \{ \} \subseteq \{ B \} \subseteq T $$
$$ \{ B \} \cup \{ B \} \subseteq \{ B \} \subseteq T$$
Analogicznie, przecięcia również należą do T:
$$ \{ B \} \cap \{ B, C \} \subseteq \{ B \} \subseteq T$$
$$ \{ B \} \cap \{ A, B, C \} \subseteq \{ B \} \subseteq T$$
$$ \{ B \} \cap \{ \} \subseteq \{ \} \subseteq T $$
$$ \{ B \} \cap \{ B \} \subseteq \{ B \} \subseteq T$$
Wszystkie warunki są spełnione. Kolekcja T jest więc poprawną topologią na X.
Drugi przykład
Ponownie rozważamy ten sam zbiór X:
$$ X = \{ A,B,C \} $$
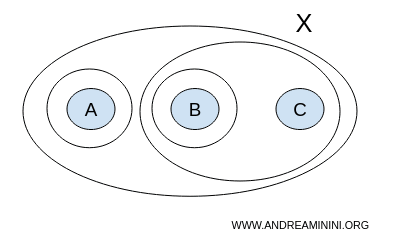
Załóżmy teraz, że rozbudowaliśmy kolekcję T o dodatkowy zbiór {A}:
$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \} \} $$
Ta kolekcja nie jest topologią, ponieważ nie jest domknięta na sumy. Na przykład:
$$\require{cancel} \{ A \} \cup \{ B \} = \{ A, B \} \cancel{\in} T $$
Mamy więc dwa zbiory uznane za otwarte ({A} i {B}), ale ich suma nie jest już otwarta, ponieważ nie znajduje się w T. Jest to sprzeczne z definicją topologii.
Wniosek jest jasny: ta kolekcja nie spełnia wymagań, więc nie może być topologią.
Na podobnej zasadzie można analizować kolejne przykłady i badać, czy dana kolekcja spełnia warunki definicyjne.