Podprzestrzeń topologiczna
Podprzestrzeń topologiczna to podzbiór przestrzeni topologicznej, na którym rozpatrujemy topologię powstałą przez ograniczenie topologii przestrzeni macierzystej. To jedno z podstawowych narzędzi, które pozwala nam analizować fragmenty większych przestrzeni bez utraty ich struktury topologicznej.
Niech \( (X, T) \) będzie przestrzenią topologiczną, gdzie \( T \) to rodzina zbiorów otwartych. Jeśli \( Y \subseteq X \), topologia indukowana na \( Y \) jest definiowana jako: \[ T_Y = \{ U \cap Y \mid U \in T \} \]
Oznacza to, że zbiór \( V \subseteq Y \) jest otwarty w topologii indukowanej wtedy i tylko wtedy, gdy można go otrzymać jako przecięcie \( Y \) ze zbiorem otwartym w \( X \).
Zbiory otwarte w podprzestrzeni zawsze mają postać \( U \cap Y \), gdzie \( U \) jest otwarty w przestrzeni macierzystej.
$$ V_{open \ in \ Y} = U \cap Y $$
Analogicznie jest ze zbiorami domkniętymi: w topologii indukowanej są to wszystkie przecięcia zbiorów domkniętych w \( X \) z podzbiorem \( Y \).
$$ V_{closed \ in \ Y} = C \cap Y $$
Uwaga: Podprzestrzeń może mieć zbiory otwarte, które nie są otwarte w całej przestrzeni. Mogą też pojawić się zbiory jednocześnie otwarte i domknięte, czyli tak zwane zbiory typu clopen.
Przykład
Weźmy zwykłą przestrzeń \( \mathbb{R} \) z jej standardową topologią, w której zbiory otwarte to przedziały otwarte.
Rozważmy podzbiór \( Y = [0,1] \).
Topologia indukowana na \( Y \) składa się ze wszystkich przecięć postaci:
$$ U \cap [0,1] $$
gdzie \( U \) jest dowolnym zbiorem otwartym w \( \mathbb{R} \).
Przykładowo, przedział \( (-1,0.5) \) jest otwarty w \( \mathbb{R} \).
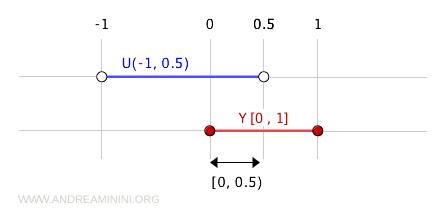
Jego przecięcie z podzbiorem \( Y \) daje:
$$ (-1,0.5) \cap [0,1] = [0,0.5) $$
W ten sposób otrzymujemy zbiór otwarty w topologii indukowanej, choć nie jest on otwarty w \( \mathbb{R} \).
Z kolei przedział domknięty \( [0,0.5] \) pozostaje domknięty także w podprzestrzeni:
$$ [-1,0.5] \cap [0,1] = [0,0.5] $$
Uwaga: Przedziały takie jak [0,a) lub (a,1], choć nie są otwarte w całej prostej, stają się otwarte w podprzestrzeni, jeśli można je otrzymać w wyniku przecięcia z odpowiednim przedziałem otwartym. Na przykład: $$ (-1,0.5) \cap [0,1] = [0,0.5) $$
Niektóre zbiory, na przykład \( (0.2,0.8) \), są otwarte zarówno w \( \mathbb{R} \), jak i w \( Y \). Podobnie \( [0.2,0.8] \) jest domknięty w obu topologiach.
Co ciekawe, cały przedział \( [0,1] \) jest w topologii indukowanej jednocześnie otwarty i domknięty.
- Dlaczego jest otwarty?
Wystarczy zauważyć, że: $$ \mathbb{R} \cap [0,1] = [0,1] $$ a \( \mathbb{R} \) jest otwarty w sobie. - Dlaczego jest domknięty?
Ponieważ: $$ [0,1] \cap [0,1] = [0,1] $$Uwaga: Dopełnienie \( [0,1] \) w \( Y \) jest puste, a zbiór pusty zawsze jest otwarty. To kolejny sposób na wykazanie domkniętości.
Zbiory jednocześnie otwarte i domknięte bywają kluczowe w wielu zagadnieniach topologicznych. Nazywamy je clopenami.
Przykład 2
Przyjrzyjmy się jeszcze jednemu klasycznemu przypadkowi.
Zbiór liczb całkowitych \( \mathbb{Z} \) traktujemy jako podzbiór \( \mathbb{R} \). Każdą liczbę całkowitą można wyodrębnić za pomocą przecięcia z odpowiednim przedziałem otwartym:
$$ (6.5,7.5) \cap \mathbb{Z} = \{7\} $$
Ten sam mechanizm działa dla dowolnej liczby całkowitej. Oznacza to, że każdy singleton w \( \mathbb{Z} \) jest otwarty w topologii indukowanej.
Idąc dalej, dowolny podzbiór \( \mathbb{Z} \) również będzie otwarty, ponieważ można go otrzymać jako przecięcie z odpowiednio dobranym przedziałem:
$$ (5.5,8.5) \cap \mathbb{Z} = \{6,7,8\} $$
Topologia indukowana na \( \mathbb{Z} \) zgadza się więc z topologią dyskretną.
Uwaga: Topologia dyskretna nie jest podtopologią topologii standardowej na \( \mathbb{R} \). Jest niezależną strukturą, ale topologia indukowana na \( \mathbb{Z} \) zachowuje się tak samo, co czyni ją z nią topologicznie równoważną.
Przykład 3
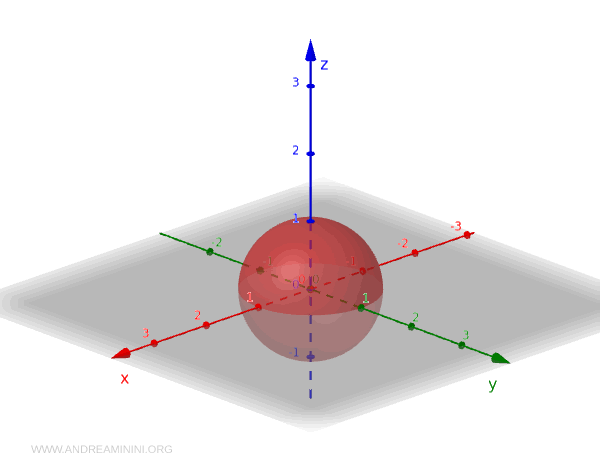
Przyjrzyjmy się teraz klasycznemu przykładowi podprzestrzeni topologicznej: sferze jednostkowej \( S^2 \) w trójwymiarowej przestrzeni euklidesowej \( \mathbb{R}^3 \). W \( \mathbb{R}^3 \) korzystamy ze standardowej topologii, w której zbiory otwarte powstają jako sumy otwartych kul. Jest to najbardziej naturalna topologia wynikająca z metryki euklidesowej.
Sfera jednostkowa jest zbiorem wszystkich punktów oddalonych dokładnie o 1 od początku układu współrzędnych:
$$ S^2 = \{ (x,y,z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1 \} $$
Topologia na \( S^2 \) jest topologią indukowaną, co oznacza, że zbiór uznajemy za otwarty na sferze wtedy i tylko wtedy, gdy można go przedstawić jako przecięcie sfery z pewnym zbiorem otwartym w \( \mathbb{R}^3 \):
$$ T_{S^2} = \{ U \cap S^2 \mid U \subseteq \mathbb{R}^3 \text{ otwarty} \} $$
Oto kilka przykładów, które pomagają zrozumieć, jak działa topologia indukowana na sferze:
- Przecięcie z dużym zbiorem otwartym
Rozważmy zbiór $$ U = \{ (x,y,z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 < 2 \}. $$ Oczywiste jest, że cała sfera mieści się w tym zbiorze. Dlatego: $$ U \cap S^2 = S^2. $$ Pokazuje to, że cała sfera jest otwarta we własnej topologii indukowanej. - Otwarty fragment sfery
Weźmy zbiór $$ U = \{ (x,y,z) \in \mathbb{R}^3 \mid z > 0 \}. $$ Jest on otwarty w \( \mathbb{R}^3 \). Jego przecięcie ze sferą to zbiór punktów sfery o dodatniej współrzędnej \( z \): $$ U \cap S^2 = \{ (x,y,z) \in S^2 \mid z > 0 \}. $$ Jest to górna półsfera, czyli klasyczny przykład zbioru otwartego w topologii sfery. - Zachowanie zbiorów otwartych
W topologii indukowanej zachodzą standardowe własności topologiczne:
- suma dowolnej liczby zbiorów otwartych na sferze jest otwarta,
- przecięcie skończonej liczby zbiorów otwartych również jest otwarte,
- zbiory \( \emptyset \) i \( S^2 \) są otwarte z definicji.
W praktyce oznacza to, że sfera, jako podprzestrzeń \( \mathbb{R}^3 \), dziedziczy topologię przestrzeni macierzystej w sposób wierny, choć ograniczony do własnej powierzchni. Każdy zbiór otwarty na sferze powstaje poprzez przecięcie otwartego zbioru trójwymiarowego z powierzchnią sfery.
Właściwości topologii indukowanej
Topologia indukowana ma kilka fundamentalnych własności, które warto zapamiętać:
- Każdy zbiór otwarty ma postać przecięcia
Jeśli zbiór jest otwarty w \( Y \), to zawsze można go zapisać jako $$ V = U \cap Y $$ dla pewnego zbioru otwartego \( U \subseteq X \). - Zbiory elementarne
Zarówno zbiór pusty, jak i cały zbiór \( Y \), są z natury otwarte, ponieważ: $$ \emptyset = \emptyset \cap Y, \quad Y = X \cap Y. $$ - Stabilność względem przecięć
Przecięcie skończonej liczby zbiorów otwartych pozostaje otwarte. Wynika to z faktu, że przecięcie skończonej liczby zbiorów otwartych w \( X \) także jest otwarte. - Stabilność względem sum
Dowolna suma zbiorów otwartych w \( Y \) jest otwarta, ponieważ suma otwartych zbiorów w \( X \) pozostaje otwarta, a następnie ograniczamy ją do podzbioru \( Y \).
Uwagi
Oto dodatkowe spostrzeżenia, które pomagają uporządkować wiedzę o topologii indukowanej:
- Topologia standardowa na dowolnym podzbiorze \( Y \subseteq \mathbb{R}^n \) pokrywa się z topologią indukowaną. Nie ma tu żadnej różnicy w strukturze otwartości.
Przykład: Niech \( Y = [-1,0) \cup (0,1] \subseteq \mathbb{R} \). Zbiory te: $$ (-1.5,0.5) \cap Y = [-1,0), $$ $$ (0,1.5) \cap Y = (0,1], $$ pokazują, że topologia standardowa na \( Y \) jest dokładnie topologią indukowaną. Co więcej, oba te zbiory są w \( Y \) jednocześnie otwarte i domknięte (czyli są clopenami), ponieważ ich dopełnienia względem \( Y \) są otwarte.
- Twierdzenie o bazie topologii indukowanej
Jeśli \( B_X \) jest bazą topologii na \( X \), to rodzina przecięć $$ B_Y = \{ B \cap Y \mid B \in B_X \} $$ stanowi bazę topologii indukowanej na \( Y \). Dzięki temu łatwo konstruować otwarte zbiory w podprzestrzeni na podstawie bazy przestrzeni macierzystej.
Topologia indukowana jest więc prostym, lecz niezwykle użytecznym narzędziem, które pozwala badać własności wybranych podzbiorów bez utraty ich topologicznej struktury.