Punkty stałe w topologii
W topologii punkt stały to argument funkcji, który pozostaje niezmieniony po jej zastosowaniu.
Intuicyjnie jest to sytuacja, w której funkcja nie przesuwa danego punktu. Jeśli dla pewnego p zachodzi f(p) = p, oznacza to, że wynik działania funkcji jest identyczny z jej wartością wejściową. Taki punkt nazywamy punktem stałym.
$$ f(p) = p $$
Aby lepiej to zobrazować, wyobraźmy sobie obrót figury wokół ustalonego punktu P.
Każdy punkt obiektu zmienia położenie w przestrzeni, ale środek obrotu pozostaje na swoim miejscu.
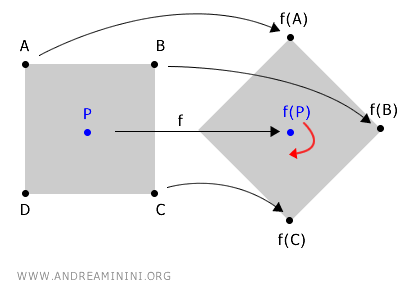
Właśnie ten punkt, oznaczony jako P, jest punktem stałym obrotu. Funkcja obrotu nie zmienia jego współrzędnych.
$$ f(P) \longrightarrow P $$
Pojęcie punktu stałego odgrywa ważną rolę w wielu obszarach matematyki i jej zastosowań. Występuje w analizie numerycznej, teorii gier, ekonomii, a także w badaniu układów dynamicznych.
Jednym z najbardziej znanych rezultatów dotyczących punktów stałych jest twierdzenie Brouwera o punkcie stałym.
Przykład: funkcja sinus
Rozważmy funkcję f(x) = sin(x) na przedziale [0, 2π].
$$ f(x) = \sin(x) $$
Wartość p = 0 jest tutaj punktem stałym, ponieważ sin(0) = 0.
$$ \sin(0) = 0 $$
Jest to przykład szczególnie prosty: funkcja zwraca dokładnie tę samą liczbę, którą otrzymała jako argument.
Przykład: funkcja cosinus
Przyjrzyjmy się teraz funkcji f(x) = cos(x) na tym samym przedziale [0, 2π].
$$ f(x) = \cos(x) $$
W tym przypadku x = 0 nie jest punktem stałym, ponieważ cos(0) = 1.
Jednak funkcja ta również posiada punkt stały. Znajduje się on w przybliżeniu w x = 0.73908513 radiana.
$$ \cos(0.73908513) = 0.73908513 $$
W tej wartości funkcja zwraca wynik praktycznie równy argumentowi, co potwierdza istnienie punktu stałego.
Twierdzenie Brouwera o punkcie stałym
Twierdzenie to stwierdza:
Każde ciągłe odwzorowanie zwartego, domkniętego obszaru n-wymiarowego w siebie ma co najmniej jeden punkt stały.
To rezultat egzystencjalny. Zapewnia istnienie punktu stałego, lecz nie mówi, gdzie dokładnie się on znajduje i jak go znaleźć.
Znaczenie tego twierdzenia jest bardzo szerokie. Leży u podstaw wielu dowodów w matematyce, a także pomaga wykazywać istnienie stanów równowagi w ekonomii i naukach o złożonych systemach.
Motyw punktów stałych powraca w wielu kontekstach, dlatego warto rozumieć jego intuicję i podstawowe przykłady.