Wnętrze zbioru
W przestrzeni topologicznej \( X \) wnętrze zbioru \( A \) to suma wszystkich podzbiorów otwartych, które mieszczą się w nim w całości. W literaturze spotyka się oznaczenia \( \text{Int}(A) \) lub \( A^\circ \).
Najprościej mówiąc, wnętrze to największy zbiór otwarty, jaki da się „wyciąć" z \( A \) bez wychodzenia poza jego granice.
Innego, większego zbioru otwartego zawartego w \( A \) po prostu nie ma.
Uwaga: Ponieważ wnętrze powstaje jako suma zbiorów otwartych, samo również jest otwarte. To bezpośrednia konsekwencja definicji.
Formalnie rzecz biorąc, wnętrze \( A \) składa się z tych punktów, które mają otwarte otoczenie pozostające w całości w \( A \).
$$ \text{Int}(A) = \bigcup \{ U \subseteq A : U \text{ jest zbiorem otwartym w } X \} $$
Punkt \( x \) należy więc do wnętrza, jeśli istnieje zbiór otwarty \( U \) taki, że \( x \in U \subseteq A \). To ujęcie świetnie pokazuje, że wnętrze zależy od topologii, a nie wyłącznie od struktury zbioru.
Kluczowa idea: Wnętrze zbioru jest zawsze pojęciem zależnym od topologii. Ta sama figura geometryczna, umieszczona w innej topologii, może mieć zupełnie inne wnętrze.
Przykład 1
Rozważmy zbiór \( A = [0,1] \) w \( \mathbb{R} \) z topologią standardową.
To klasyczny przedział domknięty: zawiera wszystkie liczby od 0 do 1, włącznie z końcami.
W tej topologii jego wnętrze to przedział otwarty \( (0,1) \):
$$ \text{Int}(A) = (0,1) $$
Punkty 0 i 1 nie mogą należeć do wnętrza, ponieważ żaden otwarty przedział nie mieści się w całości w \( [0,1] \) i jednocześnie zawiera te punkty.
Przykład 2
Spójrzmy na zbiór \( A = [0,1) \) w tej samej topologii.
Zbiór jest od lewej domknięty, a od prawej otwarty, ale wnętrze pozostaje takie samo jak poprzednio:
\[ \text{Int}(A) = (0,1) \]
Punkt 0 nadal nie wchodzi do wnętrza, ponieważ nie istnieje otwarty przedział w całości zawarty w \( [0,1) \), który by go obejmował.
Uwaga: W topologii standardowej otwarte zbiory to przede wszystkim otwarte przedziały. Ta struktura decyduje o tym, które punkty mogą należeć do wnętrza.
Przykład 3
Przenieśmy teraz zbiór \( A = [0,1) \) do przestrzeni z topologią dyskretną.
W topologii dyskretnej każdy podzbiór jest otwarty, niezależnie od jego kształtu czy liczby elementów.
Oznacza to, że każdy punkt ma „gotowe" otwarte otoczenie w \( A \).
W topologii dyskretnej otwarte są zarówno przedziały typu \( (0,0{,}5) \), jak i zbiory punktowe, zbiory skończone, przedziały domknięte oraz sam zbiór \( [0,1) \).
W takim układzie wnętrze pokrywa się ze zbiorem:
$$ \text{Int}(A) = A = [0,1) $$
To naturalna cecha topologii dyskretnej: każde wnętrze jest równe danemu zbiorowi.
Wniosek: Zmiana topologii może diametralnie zmienić wnętrze tego samego zbioru. To doskonały przykład pokazujący znaczenie otoczeń i zbiorów otwartych w topologii.
Przykład 4
Rozważmy przestrzeń \( X = \{a, b, c\} \) również z topologią dyskretną.
W tej topologii wszystkie podzbiory są otwarte: od zbioru pustego, przez singletony, aż po całe \( X \).
Dla zbioru \( A = \{b, c\} \) wnętrze to suma wszystkich otwartych zbiorów zawartych w \( A \):
\[ \text{Int}(A) = \{b\} \cup \{c\} \cup \{b, c\} = \{b, c\} \]
Wynik ponownie jest równy całemu zbiorowi.
Reguła ogólna: W topologii dyskretnej każdy zbiór jest otwarty, dlatego zawsze mamy \( \text{Int}(S) = S \) dla dowolnego podzbioru \( S \subseteq X \).
Twierdzenie o wnętrzu zbioru
W topologii jednym z kluczowych pojęć jest wnętrze zbioru. Jeśli \( S \subseteq X \) jest podzbiorem przestrzeni topologicznej \( X \), a \( y \in X \), to mówimy, że \( y \) należy do wnętrza \( S \), oznaczanego \( \operatorname{Int}(S) \), wtedy i tylko wtedy, gdy istnieje zbiór otwarty \( U \) taki, że: $$ y \in U \subseteq S. $$ To lokalne kryterium daje jasny sposób na ustalenie, czy punkt rzeczywiście leży „w środku” zbioru w sensie topologicznym.
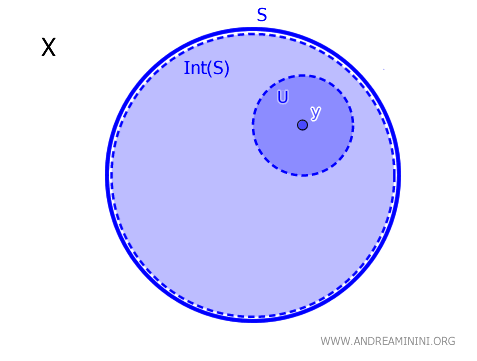
Twierdzenie to stanowi fundament wielu dalszych zagadnień, ponieważ łączy intuicyjną ideę otoczenia punktu z formalną strukturą wnętrza zbioru.
Dowód
- Warunek konieczny: Jeśli \( y \in \operatorname{Int}(S) \), to zgodnie z definicją istnieje zbiór otwarty \( U \), który zawiera punkt \( y \) i który w całości mieści się w \( S \).
- Warunek wystarczający: Jeśli istnieje zbiór otwarty \( U \) taki, że \( y \in U \subseteq S \), to punkt \( y \) należy do wnętrza \( S \), ponieważ wnętrze jest sumą wszystkich zbiorów otwartych zawartych w \( S \).
Uwaga: To twierdzenie jest jednym z podstawowych narzędzi topologii. W praktyce pozwala przełożyć intuicyjne wyobrażenie „punktu leżącego w środku zbioru” na precyzyjne kryterium matematyczne.
Przykład
Weźmy zbiór \( A = [1,3] \) w \( \mathbb{R} \) z topologią standardową.
$$ A = [1,3] $$
To przedział domknięty, obejmujący wszystkie liczby od 1 do 3 włącznie. Chcemy ustalić, które punkty są wewnętrzne.
Wyznaczanie wnętrza zbioru \( A \)
Największym otwartym podzbiorem zawartym w \( A \) jest przedział \( (1,3) \). Należy on w całości do \( A \), natomiast jego końce - 1 i 3 - nie są punktami wewnętrznymi, ponieważ każde ich otwarte otoczenie „wychodzi” poza \( A \).
W rezultacie: $$ \operatorname{Int}(A) = (1,3). $$
Uwaga: Ten przykład dobrze pokazuje różnicę między wnętrzem a domknięciem zbioru: punkty brzegowe należą do domknięcia, lecz nie do wnętrza.
Własności wnętrza zbioru
Wnętrze jest jedną z najważniejszych operacji w topologii. Poniżej przedstawiono kluczowe własności, które pomagają zrozumieć jego zachowanie oraz relacje z innymi operacjami topologicznymi.
- Unia wnętrz
Wnętrza sumują się monotonicznie: $$ \operatorname{Int}(A) \cup \operatorname{Int}(B) \subseteq \operatorname{Int}(A \cup B). $$ Często jednak suma wnętrz jest wyraźnie mniejsza niż wnętrze sumy. - Przecięcie wnętrz dwóch zbiorów
Zawsze zachodzi równość: $$ \operatorname{Int}(A) \cap \operatorname{Int}(B) = \operatorname{Int}(A \cap B). $$ - Wnętrze dopełnienia
Ważna zależność: $$ \operatorname{Int}(X - A) = X - \operatorname{Cl}(A). $$ Pokazuje to, jak wnętrze i domknięcie działają jako operacje „komplementarne”. - Domknięcie dopełnienia
Analogicznie: $$ \operatorname{Cl}(X \setminus A) = X \setminus \operatorname{Int}(A). $$
Uwagi końcowe
Kiedy bada się wnętrze zbioru, warto pamiętać o kilku istotnych zasadach:
- Każdy zbiór otwarty zawarty w \( A \) mieści się w \( \operatorname{Int}(A) \)
Wnętrze jest największym otwartym podzbiorem zawartym w \( A \), dlatego wszystko, co otwarte i zawiera się w \( A \), trafia automatycznie do jego wnętrza. - Zawieranie wnętrz w topologii
Jeśli \( A \subseteq B \), to: $$ \operatorname{Int}(A) \subseteq \operatorname{Int}(B). $$ - Kryterium otwartości
Zbiór jest otwarty dokładnie wtedy, gdy pokrywa się ze swoim wnętrzem. - Wnętrze w języku R
Język R oferuje bogate narzędzia analityczne i wizualizacyjne, które ułatwiają badanie wnętrza zbiorów, zwłaszcza w zastosowaniach statystycznych i geometrycznych.
Wnętrze jest jednym z podstawowych pojęć topologii, a znajomość jego własności pozwala lepiej rozumieć strukturę przestrzeni i zachowanie funkcji w kontekście topologicznym.