Zbiory domknięte

Zbiór $ B $ w przestrzeni topologicznej $ X $ nazywamy domkniętym, jeśli dla każdego punktu dopełnienia $ u \in X - B $ istnieje takie otoczenie tego punktu, które w całości zawiera się w dopełnieniu $ X - B $.
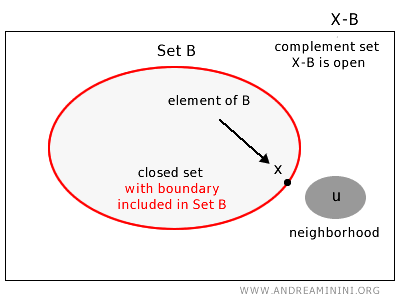
graficzny przykład zbioru domkniętego

Inaczej mówiąc, zbiór domknięty to taki, który zawiera wszystkie swoje punkty brzegowe.

Ściślej: zbiór $ B $ jest domknięty w przestrzeni topologicznej $ X $ wtedy i tylko wtedy, gdy jego dopełnienie $ X - B $ jest zbiorem otwartym.

Uwaga: Wynika z tego, że w $ B $ istnieją punkty, wokół których żadne otoczenie nie może leżeć w całości w $ B $.

Przykład na prostej rzeczywistej
Dopełnienie zbioru domkniętego
Przykład topologii skończonej
Własności zbiorów domkniętych
Przykład
Uwagi dodatkowe

Przykład na prostej rzeczywistej

Rozważmy prostą rzeczywistą $ \mathbb{R} $ i typowy przedział domknięty.

Czym jest przedział domknięty? To zbiór wszystkich punktów $ x $, dla których $ a \leq x \leq b $, gdzie $ a $ i $ b $ są liczbami rzeczywistymi spełniającymi $ a < b $. Oba końce należą do zbioru.

Przedział taki zapisujemy jako $[a,b]$, a nawiasy kwadratowe oznaczają, że zarówno $ a $, jak i $ b $, są elementami zbioru.

Na przykład przedział $[3,10]$ jest zbiorem domkniętym w $ \mathbb{R} $.

W tym przypadku zbiór $ B $ obejmuje wszystkie liczby od 3 do 10, włącznie z końcami przedziału.

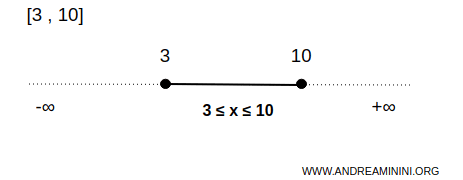
wizualizacja zbioru domkniętego i otwartego

Każdy punkt $ x $ spełniający $ 3 \leq x \leq 10 $ należy więc do zbioru, także $ x=3 $ i $ x=10 $.

Warto jednak zauważyć, że nie wszystkie punkty tego zbioru mają otoczenie w całości zawarte w $[3,10]$.

Każde otoczenie punktu $ x=3 $ zawiera bowiem również liczby mniejsze od 3, które nie należą do zbioru.

Uwaga: Nawet niezwykle małe otoczenie, np. $ 3 \pm 0{,}00000001 $, obejmuje punkty mniejsze niż 3, więc nie mieści się w całości w $[3,10]$. Analogiczna sytuacja występuje dla prawej granicy $ x=10 $.

Mamy więc klasyczny przykład zbioru domkniętego na prostej.

Zbiory domknięte na płaszczyźnie

Przenieśmy teraz tę ideę na płaszczyznę $\mathbb{R}^2$.

Rozważmy zbiór punktów spełniających nierówność:

$$ x^2 + y^2 \leq 1 $$

Opisuje ona wszystkie punkty, których odległość od środka $(0,0)$ jest mniejsza lub równa 1. Zbiór obejmuje wnętrze dysku oraz jego brzeg.

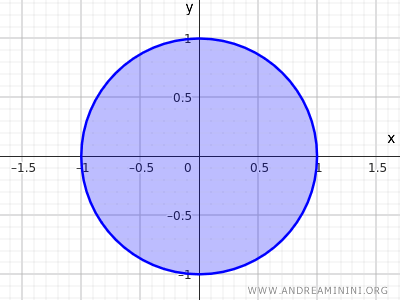
domknięty dysk jednostkowy w płaszczyźnie

Otrzymujemy w ten sposób kolejny przykład zbioru domkniętego.

Punkty leżące na okręgu $ x^2 + y^2 = 1 $ nie mają otoczeń w całości zawartych w tym zbiorze.

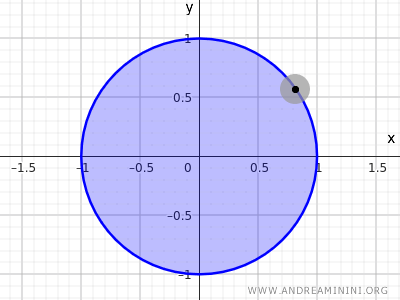
topologiczne przedstawienie zbioru domkniętego

Uwaga: Okrąg $ x^2 + y^2 = 1 $ nie jest w $ \mathbb{R}^2 $ zbiorem otwartym ani domkniętym, ponieważ zawiera jedynie punkty brzegu i nie obejmuje wnętrza. Natomiast zbiór określony przez $ x^2 + y^2 \leq 1 $, zawierający brzeg i wnętrze, jest domknięty, gdyż obejmuje wszystkie swoje punkty brzegowe.

Podobne konstrukcje można budować w trzech wymiarach (kula domknięta), a także w przestrzeniach $ n $-wymiarowych ($ n $-sfera domknięta).

Dopełnienie zbioru domkniętego

W przestrzeni topologicznej $ X $ dopełnienie zbioru domkniętego $ C $ jest zbiorem otwartym, oznaczanym jako $ X - C $.

Oznacza to, że jeśli $ C $ jest domknięty, to $ X - C $ musi być otwarty.

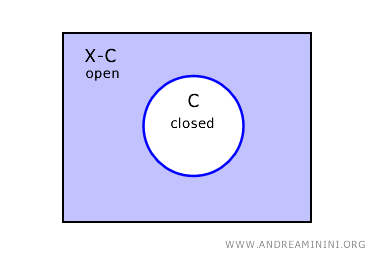
relacja pomiędzy zbiorem domkniętym a jego dopełnieniem

Analogicznie, jeśli $ U $ jest zbiorem otwartym, to jego dopełnienie $ X - U $ jest domknięte.

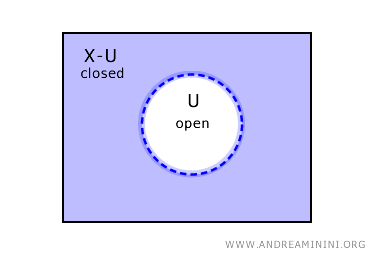
relacja pomiędzy zbiorem otwartym a jego dopełnieniem

Co istotne, istnieją również inne możliwości: w pewnych przestrzeniach topologicznych spotykamy zbiory jednocześnie otwarte i domknięte oraz zbiory, które nie są ani otwarte, ani domknięte.

Zatem brak domknięcia nie oznacza automatycznie, że zbiór jest otwarty, i odwrotnie: zbiór nieotwarty nie musi być niedomknięty.

Przykład topologii skończonej

Rozważmy przestrzeń topologiczną $ (X, T) $, w której $ X = \{a,b,c,d\} $, a topologia $ T $ składa się z następujących zbiorów otwartych:

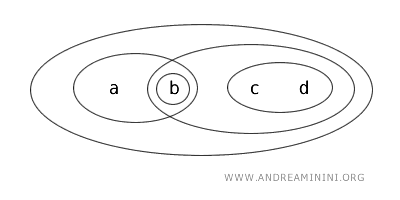
diagram skończonej przestrzeni topologicznej

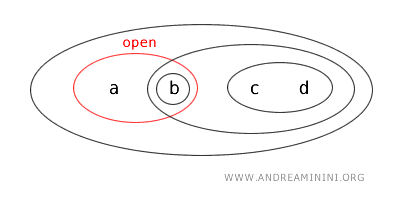
Zbiory otwarte tej topologii to: $ \{b\}, \{a,b\}, \{c,d\}, \{b,c,d\}, X $ oraz zbiór pusty $ \varnothing $.

Przeanalizujmy kilka przypadków:

Zbiór $ \{b\} $ jest otwarty, ponieważ należy do topologii jako zbiór zdefiniowany jako otwarty.
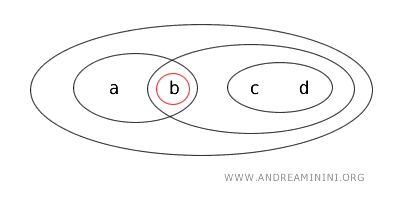
Zbiór $ \{a\} $ jest domknięty, gdyż jego dopełnienie $ X - \{a\} = \{b,c,d\} $ jest zbiorem otwartym.
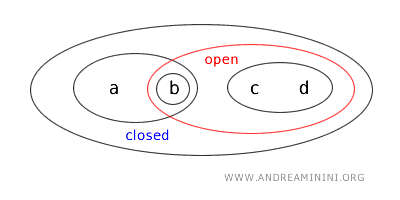
Zbiór $ \{a,b\} $ jest jednocześnie otwarty i domknięty (clopen). W topologiach na $ \mathbb{R} $ to sytuacja rzadka, lecz w bardziej ogólnych przestrzeniach możliwa. Zbiór jest otwarty z definicji topologii, a jego dopełnienie $ X - \{a,b\} = \{c,d\} $ również jest otwarte, więc zbiór jest zarazem domknięty.
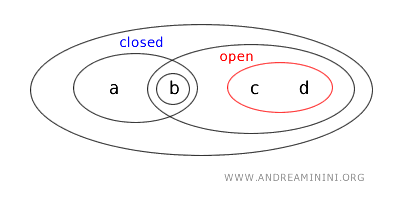
Zbiór $ \{b,c\} $ nie jest ani otwarty, ani domknięty. Nie występuje na liście zbiorów otwartych, a jego dopełnienie $ X - \{b,c\} = \{a,d\} $ również nie jest otwarte, więc zbiór nie spełnia kryteriów żadnego z tych typów.

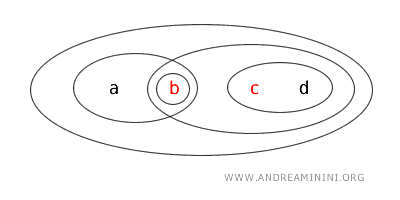
Przykład ten pokazuje, że w przestrzeni topologicznej zbiór może być otwarty, domknięty, jednocześnie otwarty i domknięty, albo nie należeć do żadnej z tych kategorii.

Własności zbiorów domkniętych

Zbiór domknięty można określić jako dopełnienie zbioru otwartego. Do jego najważniejszych własności należą:

Zbiór pusty ($\varnothing$) oraz cała przestrzeń $ X $ są zawsze zbiorami domkniętymi.
Przekrój (skończonej lub nieskończonej) rodziny zbiorów domkniętych jest również zbiorem domkniętym.
Suma skończonej liczby zbiorów domkniętych pozostaje zbiorem domkniętym.

Przykład

W standardowej topologii przestrzeni euklidesowej $ \mathbb{R}^n $ każdy punkt izolowany jest zbiorem domkniętym.

Jeżeli rozważymy punkt $ n $ na prostej rzeczywistej ($ \mathbb{R}^1 $), to jego dopełnienie stanowi zbiór wszystkich punktów rzeczywistych poza $ n $.

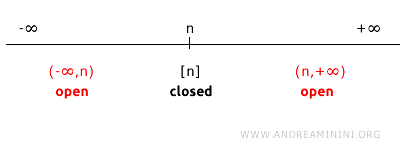
punkt izolowany jako zbiór domknięty

Dopełnienie $\{n\}$ jest sumą dwóch przedziałów otwartych: $(-\infty, n) \cup (n, +\infty)$.

Ponieważ przedziały $(-\infty, n)$ i $(n, +\infty)$ są otwarte w topologii standardowej, ich suma $(-\infty, n) \cup (n, +\infty)$ również jest zbiorem otwartym.

Zatem $\{n\}$ jest zbiorem domkniętym, ponieważ jego dopełnienie jest otwarte.

Warto jednak zauważyć, że w ogólnej topologii sytuacja ta nie musi zachodzić. Punkty izolowane nie zawsze są zbiorami domkniętymi - zależy to od struktury topologicznej danej przestrzeni.

Rozważmy topologię na $ \mathbb{R} $, generowaną przez zbiory otwarte postaci $ (n, n+1) $ dla każdego całkowitego $ n $. W tej topologii punkty izolowane $ n $ nie są zbiorami domkniętymi, ponieważ nie da się ich wyrazić jako dopełnienia zbiorów otwartych.
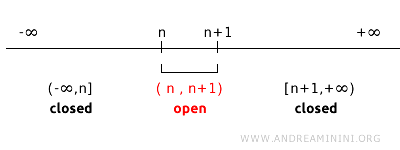
topologia, w której punkt nie jest domknięty
Na przykład zbiory $ (1,2) $ i $ (2,3) $ są w tej topologii otwarte. Dopełnienie zbioru otwartego $ (1,2) $ jest równe $ (-\infty, 1] \cup [2, +\infty) $, natomiast dopełnienie $ (2,3) $ wynosi $ (-\infty, 2] \cup [3, +\infty) $.

W tej topologii nie istnieje zbiór otwarty, którego dopełnieniem byłoby dokładnie $\{2\}$. Ogólnie, dla każdego zbioru otwartego postaci $ (n, n+1) $, jego dopełnienie jest sumą przedziałów domkniętych $ (-\infty, n] \cup [n+1, +\infty) $. Oznacza to, że punkty izolowane $ n $ nie są tu zbiorami domkniętymi, co pokazuje, jak silnie pojęcie domknięcia zależy od przyjętej topologii.

Uwagi dodatkowe

Poniżej przedstawiamy kilka uzupełniających obserwacji:

Zbiory domknięte a punkty skupienia
Punkt skupienia danego zbioru to taki punkt, którego każde otoczenie zawiera co najmniej jeden inny punkt tego zbioru. Własność ta jest kluczowa, ponieważ zbiór jest domknięty wtedy i tylko wtedy, gdy zawiera wszystkie swoje punkty skupienia.

Przykład: Przedział domknięty $[0,1]$ na osi rzeczywistej zawiera wszystkie swoje punkty skupienia.

Punkt $0{,}5$ w $[0,1]$ ma każde otoczenie zawierające nieskończenie wiele punktów tego przedziału, co potwierdza, że jest punktem skupienia.
0,5 jako punkt skupienia w przedziale domkniętym [0,1]

Taką samą własność mają punkty brzegowe. Na przykład punkt $0$ jest punktem skupienia $[0,1]$, ponieważ każde jego otoczenie zawiera inne punkty przedziału, takie jak $0{,}1$, $0{,}01$, $0{,}001$ i tak dalej.
punkty brzegowe przedziału [0,1] jako punkty skupienia
Wszystkie punkty przedziału $[0,1]$ są zatem jego punktami skupienia.

Zbiór $ A $ jest domknięty wtedy i tylko wtedy, gdy $ A = \overline{A} $
W przestrzeni topologicznej zbiór $ A $ jest domknięty, jeśli jest równy swojej domkniętości, czyli $ A = \overline{A} $. Domkniętość $ \overline{A} $ to zbiór zawierający $ A $ wraz ze wszystkimi jego punktami skupienia. Jeżeli zbiór obejmuje wszystkie swoje punkty skupienia, to jest domknięty.

I tak dalej.