Domknięcie zbioru
Domknięcie zbioru \( A \) w przestrzeni topologicznej \( X \) to część wspólna wszystkich zbiorów domkniętych, które zawierają \( A \). Zbiór ten oznacza się symbolem \( \text{Cl}(A) \).
Intuicyjnie można powiedzieć, że domknięcie zbioru \( A \) jest najmniejszym zbiorem domkniętym, który w całości obejmuje \( A \).
Nie istnieje więc żaden zbiór domknięty zawierający \( A \), który byłby od niego mniejszy.
Uwaga : Wynika to bezpośrednio z definicji. Skoro domknięcie jest częścią wspólną wszystkich zbiorów domkniętych zawierających \( A \), to automatycznie musi być najmniejszym z nich. Zawiera dokładnie te elementy, które należą do każdego takiego zbioru domkniętego.
Formalny zapis definicji domknięcia ma postać:
$$ \text{Cl}(A) = \bigcap \{ C \subseteq X : A \subseteq C \text{ oraz } C \text{ jest domknięty w } X \} $$
Symbol \( \text{Cl}(A) \) oznacza domknięcie zbioru \( A \), natomiast znak \( \bigcap \) wskazuje na część wspólną wszystkich zbiorów domkniętych \( C \), see zawierają \( A \).
Domknięcie zbioru \( A \) obejmuje zarówno wszystkie jego elementy, jak i wszystkie jego punkty skupienia w przestrzeni \( X \).
Uwaga : Warto pamiętać, że domknięcie zbioru \( A \) zależy przede wszystkim od topologii przestrzeni \( X \), a nie od samego zbioru \( A \). Ten sam zbiór, rozpatrywany w różnych topologiach, może mieć różne domknięcia.
Przykład ilustrujący pojęcie
Rozważmy zbiór \( A = (0, 1) \) w przestrzeni \( \mathbb{R} \), wyposażonej w topologię standardową.
Jest to przedział otwarty, zawierający wszystkie liczby rzeczywiste ściśle pomiędzy 0 a 1, bez punktów krańcowych.
W tym przypadku domknięciem zbioru \( A \) jest przedział \( [0, 1] \).
$$ \text{Cl}(A) = [0,1] $$
Otrzymany zbiór zawiera zarówno przedział \( (0,1) \), jak i jego punkty skupienia, czyli końce przedziału: 0 oraz 1.
Uwaga : W topologii standardowej na \( \mathbb{R} \) zbiór jest domknięty wtedy i tylko wtedy, gdy zawiera wszystkie swoje punkty skupienia. Punkt jest punktem skupienia, jeżeli w każdym jego otoczeniu znajduje się co najmniej jeden inny punkt tego zbioru. Przykładowo, część wspólna przedziałów domkniętych [0,2] oraz [-1,1] jest równa [0,1]. $$ [0,2] \cap [-1,1]=[0,1] $$ Nie istnieje mniejszy przedział domknięty, który zawierałby \( (0,1) \).
Przykład 2
Rozważmy teraz zbiór \( A = [0, 1) \) w przestrzeni \( \mathbb{R} \), nadal z topologią standardową.
Jest to przedział domknięty z lewej strony i otwarty z prawej, zawierający wszystkie liczby rzeczywiste od 0 włącznie do 1, z wyłączeniem punktu 1.
Domknięciem tego zbioru jest ponownie przedział \( [0,1] \).
$$ \text{Cl}(A) = [0,1] $$
Punkt 0 należy już do zbioru \( A \), natomiast punkt 1 nie należy do niego, lecz jest jego punktem skupienia.
Dlatego domknięcie zbioru \( A \) musi zawierać również prawy kraniec, co prowadzi do zbioru domkniętego \( [0,1] \), najmniejszego możliwego zbioru domkniętego zawierającego \( A \).
Uwaga : Przykład ten dobrze pokazuj/pl/math/domknicie-podzbioru-zbioru-domknitegoe sens definicji domknięcia jako zbioru obejmującego wszystkie punkty skupienia. Ponownie można zauważyć, że $$ [0,2] \cap [-1,1]=[0,1] $$
Przykład 3
Rozważmy ten sam zbiór \( A = [0,1) \), lecz tym razem w przestrzeni \( X \) wyposażonej w topologię dyskretną.
W topologii dyskretnej każdy podzbiór przestrzeni jest jednocześnie zbiorem otwartym i domkniętym.
- Zbiór otwarty
Każdy podzbiór \( X \) jest zbiorem otwartym, a więc także \( A \). - Zbiór domknięty
Każdy podzbiór \( X \) jest również domknięty, ponieważ jego dopełnienie jest zbiorem otwartym. W szczególności \( A \) jest zbiorem domkniętym.
Oznacza to, że każdy zbiór jest tutaj jednocześnie otwarty i domknięty (ang. clopen).
W tej sytuacji domknięcie zbioru \( A \) pokrywa się z samym \( A \).
$$ \text{Cl}(A) = [0,1) $$
Najmniejszym zbiorem domkniętym zawierającym \( A \) jest więc po prostu \( A \).
Uwaga : Ten przykład wyraźnie pokazuje, jak istotną rolę odgrywa topologia przestrzeni. To ona, a nie sam zbiór, decyduje o tym, które punkty należą do jego domknięcia.
Przykład 4
Rozważmy przestrzeń topologiczną \( X = \{a, b, c\} \) z topologią dyskretną.
W tym przypadku każdy podzbiór \( X \) jest zbiorem otwartym:
- \( \emptyset \) oraz \( \{a, b, c\} \) są otwarte z definicji.
- Zbiory jednopunktowe \( \{a\} \), \( \{b\} \), \( \{c\} \) również są otwarte.
- Dowolne ich kombinacje, takie jak \( \{a, b\} \), \( \{a, c\} \) czy \( \{b, c\} \), są także zbiorami otwartymi.
Ponieważ dopełnienie dowolnego podzbioru jest również zbiorem otwartym, wszystkie podzbiory są jednocześnie otwarte i domknięte.
Weźmy zbiór \( A = \{b, c\} \). Jest on otwarty i jednocześnie domknięty, gdyż jego dopełnienie \( X/A = \{a\} \) jest zbiorem otwartym.
Domknięcie zbioru \( A \), oznaczane przez \( \text{Cl}(A) \), jest częścią wspólną wszystkich zbiorów domkniętych zawierających \( A \). W tym przypadku nie zachodzi potrzeba dodawania nowych elementów.
\[ \text{Cl}(A) = \{b, c\} \]
W topologii dyskretnej każdy zbiór jest już domknięty, dlatego jego domknięcie zawsze pokrywa się ze zbiorem wyjściowym.
Uwaga : Dla pełnej jasności można zauważyć, że jedynymi zbiorami domkniętymi zawierającymi \( A \) są \( \{b, c\} \) oraz \( \{a, b, c\} \). $$ \text{Cl}(A) = \{b, c\} \cap \{a, b, c\} = \{b, c\} $$ Część wspólna daje dokładnie \( A \), a więc \( \text{Cl}(A) = A \).
Twierdzenie o domknięciu zbioru
W przestrzeni topologicznej \( X \) punkt \( y \) należy do domknięcia podzbioru \( S \), oznaczanego przez \( \text{Cl}(S) \), wtedy i tylko wtedy, gdy każdy zbiór otwarty \( U \), który zawiera punkt \( y \), ma niepuste przecięcie ze zbiorem \( S \). Zapisujemy to w postaci: \( y \in \text{Cl}(S) \iff \forall \ U \text{ otwarty, } y \in U \Rightarrow U \cap S \neq \emptyset \).
Mówiąc prościej, punkt \( y \in X \) należy do domknięcia zbioru \( S \), jeżeli w każdym jego otwartym otoczeniu znajdziemy przynajmniej jeden element zbioru \( S \).
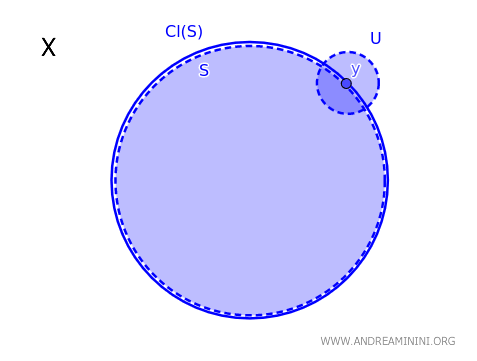
Twierdzenie to daje wygodne i bardzo intuicyjne kryterium pozwalające sprawdzić, czy dany punkt należy do domknięcia zbioru w przestrzeni topologicznej.
Dowód
- Warunek konieczny : Jeżeli \( y \in \text{Cl}(S) \), to z definicji domknięcia wynika, że każdy zbiór otwarty zawierający punkt \( y \) musi przecinać się ze zbiorem \( S \). Domknięcie obejmuje bowiem zarówno punkty należące do zbioru \( S \), jak i jego punkty skupienia. Punkt skupienia to taki punkt, którego każde otoczenie zawiera co najmniej jeden punkt zbioru \( S \).
- Warunek wystarczający : Jeżeli natomiast każdy zbiór otwarty zawierający \( y \) ma niepuste przecięcie ze zbiorem \( S \), to punkt \( y \) jest albo elementem zbioru \( S \), albo jego punktem skupienia. W obu przypadkach należy on do \( \text{Cl}(S) \), ponieważ nie istnieje jego otoczenie otwarte rozłączne ze zbiorem \( S \).
Uwaga : Twierdzenie to jest jednym z podstawowych rezultatów topologii ogólnej. Pokazuje ono ścisły związek pomiędzy pojęciem zbioru otwartego a pojęciem domknięcia. Jest ono szeroko wykorzystywane przy badaniu ciągłości funkcji, zbieżności ciągów, filtrów i sieci, a także w wielu klasycznych argumentach topologicznych.
Przykład
Rozważmy zbiór \( A = (0, 2) \) w topologii standardowej na \( \mathbb{R} \), czyli otwarty przedział liczb rzeczywistych.
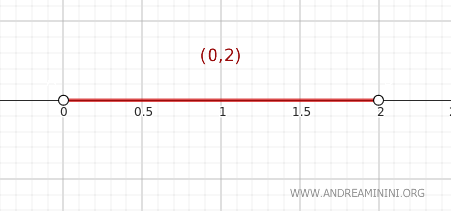
Zastosujmy twierdzenie, aby sprawdzić, czy dany punkt \( y \) należy do \( \text{Cl}(A) \).
Wybierzmy punkt \( y = 2 \in \mathbb{R} \).
Zgodnie z treścią twierdzenia, punkt \( y \) należy do \( \text{Cl}(A) \) wtedy i tylko wtedy, gdy każdy zbiór otwarty zawierający \( y \) przecina się ze zbiorem \( A \).
- Analiza otoczeń punktu \( y \) : Każdy przedział otwarty zawierający punkt \( y = 2 \), na przykład \( (1{,}9, 2{,}1) \), \( (1{,}95, 2{,}05) \) czy \( (1{,}99, 2{,}01) \), zawiera punkty należące do zbioru \( A = (0, 2) \), takie jak \( 1{,}95 \) lub \( 1{,}99 \).
- Wniosek : Skoro każde otoczenie otwarte punktu \( y = 2 \) zawiera elementy zbioru \( A \), wynika stąd, że punkt \( y = 2 \) rzeczywiście należy do \( \text{Cl}(A) \).
Ostatecznie punkt \( y = 2 \) należy do domknięcia zbioru \( A \), ponieważ żadne jego otoczenie nie jest całkowicie rozłączne ze zbiorem \( A \).
$$ y \in \text{Cl}(A) $$
Widzimy więc, że domknięciem zbioru \( A \) jest przedział domknięty \( \text{Cl}(A) = [0, 2] \), który w szczególności zawiera punkt \( y = 2 \).
Własności domknięcia w przestrzeniach topologicznych
Poniżej zestawiono najważniejsze własności domknięcia w przestrzeni topologicznej oraz podstawowe relacje między domknięciem a wnętrzem zbioru, które często okazują się zaskakujące przy pierwszym kontakcie.
- Wnętrze dopełnienia i dopełnienie domknięcia
Wnętrze dopełnienia zbioru \( A \) jest równe dopełnieniu jego domknięcia: $$ \operatorname{Int}(X - A) = X - \operatorname{Cl}(A) $$ - Domknięcie dopełnienia i dopełnienie wnętrza
Domknięcie dopełnienia zbioru \( A \) pokrywa się z dopełnieniem jego wnętrza: $$ \operatorname{Cl}(X - A) = X - \operatorname{Int}(A) $$
Istotne obserwacje
Poniżej przedstawiono kluczowe własności operatora domknięcia wraz z krótkim komentarzem pojęciowym :
- Jeżeli \( C \) jest zbiorem domkniętym w \( X \) oraz \( A \subseteq C \), to \( \text{Cl}(A) \subseteq C \)
Domknięcie zbioru \( A \), jako najmniejszy zbiór domknięty zawierający \( A \), musi zawierać się w każdym zbiorze domkniętym, który zawiera \( A \). - Jeżeli \( A \subseteq B \), to \( \text{Cl}(A) \subseteq \text{Cl}(B) \)
Operator domknięcia jest monotoniczny względem relacji zawierania zbiorów. - Zbiór \( A \) jest domknięty wtedy i tylko wtedy, gdy \( A = \text{Cl}(A) \)
Zbiór jest domknięty dokładnie wówczas, gdy zawiera wszystkie swoje punkty przyległe, czyli gdy pokrywa się ze swoim domknięciem. - Domknięcie zbioru jest sumą zbioru i jego punktów skupienia
Jeżeli \( A' \) oznacza zbiór punktów skupienia zbioru \( A \), to zachodzi równość: $$ \text{Cl}(A) = A \cup A' $$ - Idempotentność
Wielokrotne zastosowanie operatora domknięcia nie zmienia otrzymanego wyniku: $$ \text{Cl}(\text{Cl}(A)) = \text{Cl}(A) $$ - Zawieranie zbioru wyjściowego
Każdy zbiór zawiera się w swoim domknięciu: $$ A \subseteq \text{Cl}(A) $$
Kolejne materiały zostaną przedstawione wkrótce.