Podstawa Topologii

Podstawa topologii to rodzina \( B \) zbiorów otwartych, z której można odtworzyć całą topologię \( T \), zapisując każdy zbiór otwarty jako sumę elementów należących do \( B \).

Niech \( X \) będzie zbiorem, a \( T \) - topologią zdefiniowaną na \( X \). W takim układzie podstawą topologii \( T \) nazywamy rodzinę \( B \), której elementy, czyli zbiory bazowe, spełniają dwa warunki:

• Każdy punkt \( x \in X \) należy do co najmniej jednego zbioru z \( B \).
• Jeśli \( x \in B_1 \cap B_2 \), gdzie \( B_1, B_2 \in B \) i przecięcie to nie jest puste, to istnieje \( B_3 \in B \) takie, że \( x \in B_3 \subseteq B_1 \cap B_2 \). Oznacza to, że w każdym niepustym przecięciu dwóch zbiorów bazowych obecny jest kolejny zbiór bazowy obejmujący dany punkt.
  

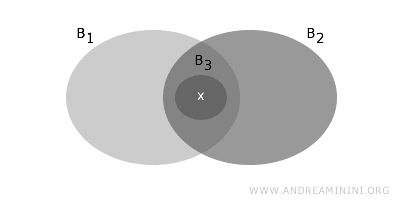
Warunki te są dokładnie tymi, które zapewniają, że rodzina \( B \) rzeczywiście generuje topologię \( T \).

Dlaczego jest to istotne ?

Podstawa pozwala opisać topologię w sposób zwarty i przejrzysty. Zamiast operować na wszystkich zbiorach otwartych, które nierzadko tworzą złożoną strukturę, wystarczy wskazać rodzinę zbiorów „pierwotnych”, z których pozostałe można zbudować przez branie sum.

Uwaga: Warunek dotyczący przecięć gwarantuje zgodność z aksjomatami topologii, w szczególności z faktem, że przecięcie dwóch zbiorów otwartych również jest otwarte.

Przykład elementarny

Rozważmy zbiór:

$$ X = \{a, b, c \} $$

oraz topologię:

$$ T = \{ \emptyset, \{ a \}, \{ b,c \}, \{ a,b,c \} \} $$

Jest to pełna lista zbiorów otwartych zdefiniowanych na \( X \).

Jedna z poprawnych podstaw tej topologii to:

$$ B = \{ \{ a \}, \{ b,c \} \} $$

Rodzina ta spełnia oba warunki definicji: każdy punkt należy do jakiegoś zbioru bazowego, a wszystkie zbiory otwarte można zrekonstruować jako sumy elementów z \( B \).

Przykłady:

• \( \{a\} \in B \)
• \( \{b,c\} \in B \)
• \( \{a,b,c\} = \{a\} \cup \{b,c\} \)

Uwaga: Zbiór pusty (Ø) jest podzbiorem nieodpowiednim dowolnego zbioru, a więc w każdej topologii występuje jako zbiór otwarty: $$ \emptyset \in T $$

Przykład ten w klarowny sposób ilustruje pojęcie podstawy dla zbiorów skończonych. W przypadku zbiorów nieskończonych idea pozostaje taka sama, choć konstrukcja odpowiedniej podstawy może wymagać więcej uwagi.

Inna perspektywa

Inną poprawną podstawą tej samej topologii jest rodzina:

$$ B = \{ \{ a \}, \{ b \}, \{ c \} \} $$

Są to singlety zbioru \( X \).

Sprawdźmy, że rzeczywiście generują topologię \( T = \{ \varnothing, X, \{a\}, \{b,c\} \} \):

• \( \varnothing \) należy do każdej topologii.
• \( \{a\} \in B \)
• \( \{b,c\} = \{b\} \cup \{c\} \)
• \( X = \{a,b,c\} = \{a\} \cup \{b\} \cup \{c\} \)

Uwaga: Ten przykład pokazuje, że jedna topologia może mieć wiele różnych podstaw, z których każda daje inny, równie poprawny sposób opisu rodziny zbiorów otwartych.

Przykład 2

W przypadku prostej rzeczywistej rolę podstawy topologii standardowej pełni rodzina wszystkich otwartych przedziałów:

$$ B = \{ (a,b) \subseteq \mathbb{R} \mid a < b \} $$

Każdy punkt \( \mathbb{R} \) należy do pewnego przedziału otwartego, a przecięcie dwóch takich przedziałów zawierających dany punkt zawsze zawiera kolejny przedział otwarty obejmujący ten punkt.

Przykładowo przecięcie \( (0,3) \) i \( (2,4) \) to przedział \( (2,3) \):

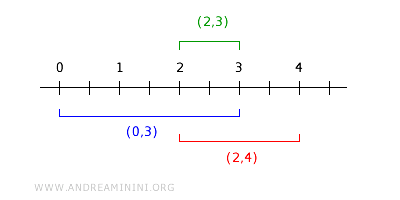
$$ (0,3) \cap (2,4) = (2,3) \in B $$ co dobrze ilustruje działanie warunku przecięcia.

Uwagi końcowe

Oto kilka dodatkowych spostrzeżeń dotyczących podstaw topologicznych:

• Jeśli jako podstawę \( B \) zbioru \( X \) przyjmujemy wszystkie singlety \( \{x\} \), to ich sumy pozwalają wygenerować bardzo różne topologie na \( X \).

  Na przykład dla podstawy \( B = \{ \{a\}, \{b\}, \{c\} \} \) otrzymujemy topologię \( T = \{ \varnothing, \{a\}, \{b,c\}, X \} \).
  
  Jednak ta sama podstawa może prowadzić do innych topologii, m.in.:
  • \( T = \{ \varnothing, \{b\}, \{a,c\}, X \} \)
  • Topologia trywialna \( T = \{ \varnothing, X \} \)
  • Topologia dyskretna \( T = \{ \varnothing, \{a\}, \{b\}, \{c\}, \{a,b\}, \{a,c\}, \{b,c\}, X \} \)

  Uwaga: Pierwszy warunek definicji jest spełniony, gdyż każdy punkt ma odpowiadający mu singleton. Drugi natomiast jest automatycznie prawdziwy, ponieważ singlety są rozłączne i każdy zawiera tylko jeden element.

Zasada działania podstaw jest ogólna i obowiązuje zarówno w przestrzeniach skończonych, jak i nieskończonych. Niezależnie od natury zbioru, topologia generowana przez wybraną rodzinę bazową powstaje zawsze przez te same mechanizmy.