Zbiory, które nie są ani otwarte, ani domknięte

W topologii istnieją zbiory, które nie spełniają warunków wymaganych do uznania ich za otwarte lub domknięte. Takie obiekty zajmują miejsce pomiędzy obiema kategoriami i stanowią ważny element teorii.

Sytuacja ta pojawia się wtedy, gdy dany zbiór nie jest zbiorem otwartym ani dopełnieniem zbioru otwartego. W takiej konfiguracji nie można go również zaklasyfikować jako zbiór domknięty.

Uwaga: W codziennych przykładach, opartych na zbiorze liczb rzeczywistych, łatwo ulec wrażeniu, że każdy zbiór musi być albo otwarty, albo domknięty. W szerszym ujęciu topologicznym struktura jest znacznie bogatsza i takie przypadki pojawiają się w sposób naturalny. Poniższy przykład pokazuje to w najprostszej możliwej formie.

Przykład

Weźmy zbiór \( X = \{a,b,c,d\} \) oraz topologię \( T \), w której zbiorami otwartymi są: \( \{b\} \), \( \{a,b\} \), \( \{c,d\} \), \( \{b,c,d\} \), \( \{a,b,c,d\} \) oraz zbiór pusty (Ø).

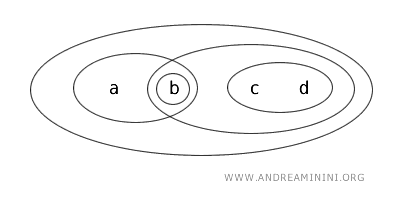
Przyjrzyjmy się podzbiorowi \( \{b,c\} \subset X \). Nie należy on do rodziny zbiorów otwartych, więc nie jest otwarty. Z kolei jego dopełnienie \( X \setminus \{b,c\} = \{a,d\} \) również nie jest otwarte, dlatego \( \{b,c\} \) nie jest też zbiorem domkniętym.

W tej topologii otrzymujemy zatem przykład zbioru, który nie jest ani otwarty, ani domknięty. Podobne konstrukcje można znaleźć w wielu przestrzeniach topologicznych, szczególnie wtedy, gdy struktura jest bogatsza niż ta znana z prostych przykładów na liczbach rzeczywistych.