Topologia

Topologia jest działem matematyki zajmującym się badaniem tych własności przestrzeni, które pozostają niezmienne przy deformacjach ciągłych, takich jak rozciąganie, zginanie czy skręcanie, pod warunkiem że obiekt nie zostaje rozerwany ani sztucznie sklejony.

Z takiego punktu widzenia topologia nie skupia się na dokładnym kształcie obiektów, lecz na ich strukturze i zachowaniu pod wpływem przekształceń ciągłych.

Zmiana badanych własności jest możliwa wyłącznie w wyniku operacji nieciągłych, na przykład wtedy, gdy fragment przestrzeni zostaje przecięty albo gdy dwie rozłączne części zostają ze sobą połączone.

Klasycznym przykładem są kula i sześcian, które są topologicznie równoważne. Jedną figurę można przekształcić w drugą za pomocą deformacji ciągłej, bez konieczności rozcinania czy sklejania.

Przeciwnie, kula i torus nie są topologicznie równoważne, ponieważ przejście od jednej figury do drugiej wymagałoby utworzenia lub usunięcia otworu, co nieuchronnie wiąże się z operacją cięcia albo sklejania.

Innymi słowy, topologia bada przede wszystkim sposób, w jaki przestrzenie są zorganizowane i jak ich części są ze sobą powiązane, a nie wielkości metryczne, takie jak odległość, rozmiar czy dokładny kształt.

W tym ujęciu pojęcia długości, pola powierzchni, objętości czy miary kątów tracą swoje kluczowe znaczenie. Najważniejsze stają się jakościowe własności figur oraz możliwość ich wzajemnego przekształcania za pomocą deformacji ciągłych.

Tak rozumiana topologia obejmuje między innymi spójność, zwartość, liczbę otworów obiektu, a także inne globalne własności przestrzeni.

Centralnym pojęciem tej dziedziny jest przestrzeń topologiczna. Jej podstawowymi przekształceniami są homeomorfizmy, czyli odwzorowania ciągłe i bijektywne, których odwrotność również jest ciągła, umożliwiające modyfikację przestrzeni przy zachowaniu jej struktury topologicznej.

Z tego powodu topologia bywa często określana mianem „geometrii gumowej kartki”. Obiekty wyobraża się jako wykonane z elastycznego materiału, który można rozciągać, zginać lub ściskać, lecz nie wolno go rozrywać ani sklejać. Współcześnie topologia stanowi jeden z fundamentalnych i silnie jednoczących obszarów nowoczesnej matematyki.

Od mostów Eulera do nowoczesnej matematyki

Historia topologii zaczyna się w XVIII wieku od słynnego problemu Siedmiu Mostów w Królewcu. Leonhard Euler zauważył wtedy coś genialnego: aby rozwiązać problem przechodzenia przez wszystkie mosty dokładnie raz, nie trzeba znać odległości, a jedynie połączenia między punktami.

Tak narodziła się idea, że to nie kształt, lecz struktura połączeń jest kluczowa - fundament całej topologii.

Problem Siedmiu Mostów: w mieście z siedmioma mostami należało znaleźć trasę, która pozwala przejść przez każdy most dokładnie raz.

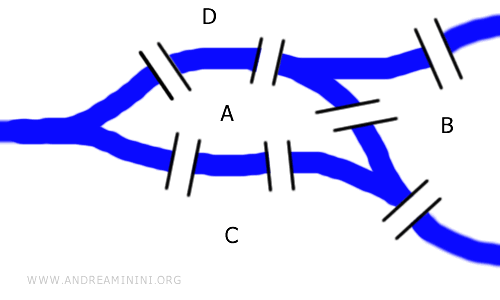
Nie liczyły się długości mostów - tylko to, które punkty łączą. Euler zamienił mapę miasta w graf, czyli sieć połączeń.

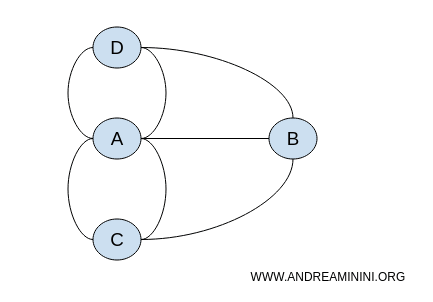
Wierzchołki grafu można ustawić dowolnie - jego istota nie zmienia się. Każdy układ z tymi samymi połączeniami jest topologicznie równoważny.

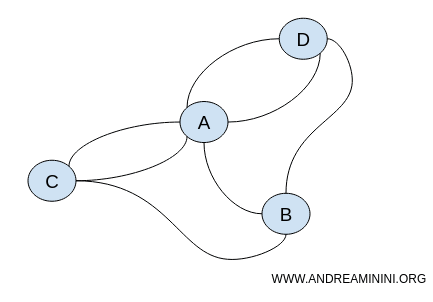
To właśnie ciągłość i spójność, nie odległość, decydują o strukturze przestrzeni.

Euler dowiódł, że zadanie jest nierozwiązywalne - i w ten sposób stworzył pierwsze narzędzie topologii. W XIX wieku jego idee rozwinęli m.in. Gauss, Möbius, Listing, Riemann i Klein.

Ciekawostka: Johann Listing w 1847 roku wprowadził słowo „topologia”. Dopiero po latach termin ten stał się powszechny w nauce.

Później Henri Poincaré dał tej dziedzinie nową głębię, tworząc topologię algebraiczną. A w XX wieku badania Hausdorffa, Cantora i Brouwera nadały jej nowoczesną, abstrakcyjną formę.

Dziś topologia jest nie tylko teorią - to język współczesnej matematyki, fizyki i informatyki, używany do opisu przestrzeni, sieci i kształtów o dowolnej złożoności.

Przestrzeń topologiczna - matematyka połączeń

Przestrzeń topologiczna to zbiór X, w którym określamy rodzinę T podzbiorów zwaną „topologią”. Dzięki niej można mówić o pojęciach takich jak ciągłość, bliskość czy granica w sposób dużo bardziej ogólny niż w klasycznej geometrii.

$$ (X,T) $$

Przykład: prosta rzeczywista \( \mathbb{R} \) z topologią standardową. Zbiór jest otwarty, jeśli wokół każdego punktu można znaleźć mały przedział zawarty w tym zbiorze. To właśnie na tej idei opiera się pojęcie ciągłości w topologii.

Homeomorfizmy - ciągłe przekształcenia

Homeomorfizm to ciągłe, odwracalne przekształcenie między dwiema przestrzeniami topologicznymi, które zachowuje ich strukturę. Dwie przestrzenie są topologicznie równoważne, jeśli można jedną płynnie przekształcić w drugą.

Przykład: klasyczne porównanie filiżanki i pączka (torusa). Oba obiekty mają po jednym otworze i można je „zamienić miejscami” poprzez ciągłe deformacje, bez rozrywania czy sklejania.

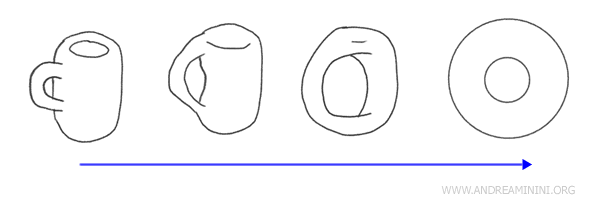
Geometria a topologia - dwie perspektywy

Geometria i topologia patrzą na przestrzeń w zupełnie różny sposób, ale doskonale się uzupełniają.

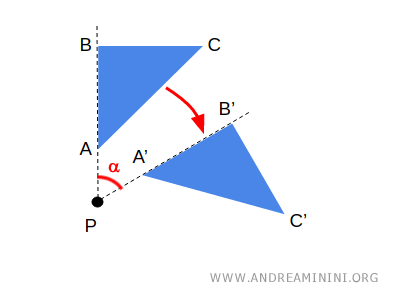
• Geometria bada kształty mierzalne - długości, kąty, odległości. Interesuje ją, jak figury wyglądają i jak można je przekształcać bez zmiany wymiarów. Przykładem jest obrót figury, który zachowuje odległości.
  

  Najbardziej znana jest geometria euklidesowa, ale istnieją też geometrie nieeuklidesowe - badające światy, w których piąty postulat Euklidesa (o prostych równoległych) przestaje obowiązywać.

• Topologia bada kształty „gumowe” - te, które można deformować bez zrywania połączeń. Nie interesuje jej, ile coś mierzy, lecz jak jest połączone. Jeśli sześcian z gliny uformujesz w kulę bez dodawania ani odejmowania materiału, wciąż masz ten sam obiekt topologiczny.
  

  Przykład: kulka i sześcian są homeomorficzne, bo można jeden płynnie przekształcić w drugi. Takie przekształcenia - bez cięcia i sklejania - są esencją topologii.
  

W pewnym sensie topologia to geometria bez miarki - bada nie to, co widzimy, lecz to, jak rzeczy są ze sobą połączone.

Najważniejsze działy topologii

Dziś topologia to rozbudowana dziedzina o wielu specjalizacjach, od teorii czysto matematycznych po praktyczne zastosowania.

• Topologia geometryczna - bada własności niezmienne przy rozciąganiu, ściskaniu i zginaniu. Interesuje ją ciągłość, spójność i zwartość, bez odniesienia do pojęcia odległości.
• Topologia ogólna (zwana też topologią zbiorów punktowych) - formułuje najbardziej podstawowe definicje i prawa rządzące przestrzeniami. Bada zbiory otwarte i domknięte, pojęcie ciągłości i granicy.
• Topologia algebraiczna - łączy topologię z algebrą, przypisując przestrzeniom obiekty algebraiczne, które pomagają zrozumieć ich strukturę.
• Topologia różniczkowa - używa rachunku różniczkowego do badania przestrzeni przypominających lokalnie przestrzeń euklidesową, wprowadzając pojęcia takie jak krzywizna i styczność.
• Topologia stosowana - wykorzystuje idee topologiczne w praktyce: w analizie danych, sieciach neuronowych, inżynierii czy biologii obliczeniowej.

Każda z tych dziedzin pokazuje, że topologia to nie tylko teoria - to uniwersalny język struktur, który pozwala zrozumieć zarówno świat matematyki, jak i rzeczywistość wokół nas.