Zbiory otwarte w topologii

Zbiór A nazywamy otwartym, jeśli dla każdego punktu x należącego do A (x∈A) istnieje takie otoczenie tego punktu, które w całości zawiera się w A.

 

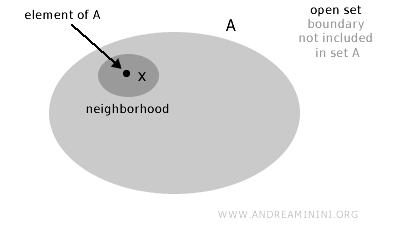
Innymi słowy, zbiór jest otwarty, jeśli jego „granica" pozostaje na zewnątrz, a żaden punkt brzegowy nie należy do samego zbioru.

Ściślej mówiąc, zbiór A w przestrzeni topologicznej X jest otwarty, gdy dla każdego punktu x∈A można wskazać otoczenie x w całości zawarte w A.

Uwaga. Oznacza to, że wokół każdego punktu zbioru da się wybrać „obszar", który leży całkowicie w jego wnętrzu i nie styka się z jego granicą.

Przykład praktyczny

Najprostszym przykładem zbioru otwartego na prostej jest przedział otwarty.

Czym jest przedział otwarty? Przedział otwarty w R to zbiór liczb rzeczywistych x spełniających warunek a < x < b, gdzie a i b są rzeczywiste oraz a < b.

Przedział taki zapisujemy (a,b). Nawiasy okrągłe oznaczają, że punkty a i b nie należą do zbioru.

Na przykład (3,10) jest zbiorem otwartym na osi liczbowej.

W tym przypadku A zawiera nieskończenie wiele punktów pomiędzy 3 a 10, z wyłączeniem obu końców.

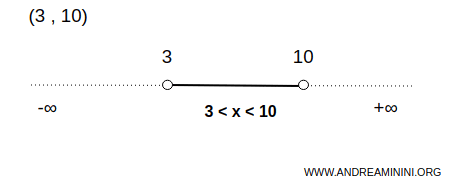
Oznacza to, że dla dowolnego punktu x z tego przedziału można zawsze znaleźć mniejszy przedział otwarty leżący w całości w (3,10).

Na przykład dla x=3.1 można wybrać przedział (3.09,3.11), który w całości mieści się w (3,10).

Podobnie dla każdego innego punktu wewnątrz (3,10), ponieważ między dowolnymi dwiema liczbami rzeczywistymi istnieje nieskończenie wiele innych liczb.

Uwaga. Nawet dla punktu takiego jak 3.001 można wybrać otoczenie 3.001±0.00000001, które wciąż leży w całości w (3,10) i zawiera nieskończenie wiele liczb.

To klasyczny przykład zbioru otwartego w jednym wymiarze.

Inne przykłady

Ten sam pomysł obowiązuje również w przestrzeni dwuwymiarowej, na przykład na płaszczyźnie.

Rozważmy zbiór punktów wewnątrz okręgu o promieniu r=1 i środku w punkcie (0,0):

$$ x^2+y^2<1 $$

Nierówność ta opisuje wszystkie punkty, których odległość od środka jest mniejsza niż 1. Uwzględnia wnętrze koła, ale odrzuca punkty leżące na jego brzegu.

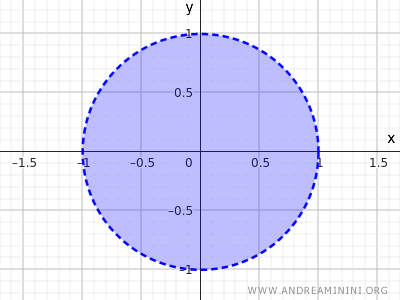
To kolejny przykład zbioru otwartego.

Kiedy zbiór jest domknięty?

Zbiór domknięty otrzymujemy, jeśli dołączymy do niego punkty leżące na okręgu.

$$ x^2+y^2 \le 1 $$

Wtedy warunek otwartości przestaje być spełniony, ponieważ punkty brzegowe nie mają otoczeń w całości zawartych w zbiorze.

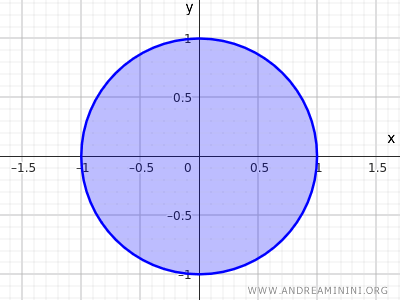
W zbiorze domkniętym punkty brzegowe nie posiadają otoczenia mieszczącego się w całości w tym zbiorze.

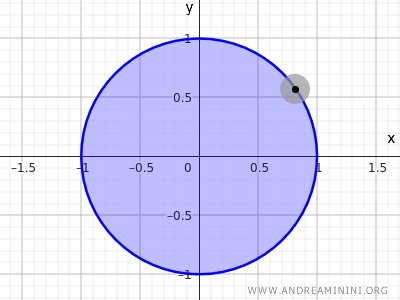
Uwaga. Równanie \(x^2+y^2=1\) nie opisuje w R² ani zbioru otwartego, ani domkniętego, ponieważ uwzględnia wyłącznie punkty na brzegu. Z kolei zbiór \(x^2+y^2<1\) jest otwarty, a \(x^2+y^2\le 1\) stanowi przykład zbioru domkniętego.

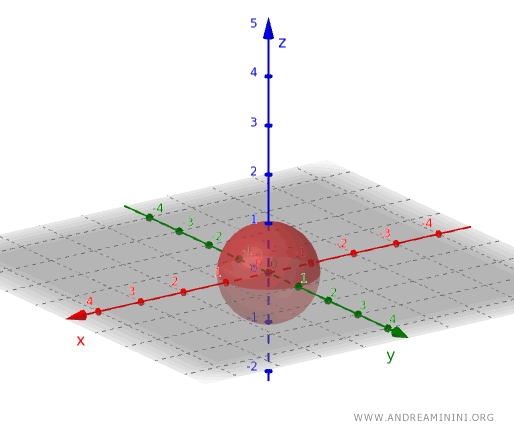
Analogicznie, w przestrzeni trójwymiarowej zbiorem otwartym będzie wnętrze kuli, bez punktów leżących na jej powierzchni.

Wybór topologii

Przedziały otwarte są intuicyjne i stanowią dobry punkt wyjścia, ale pojęcie zbioru otwartego jest znacznie głębsze.

Po zrozumieniu prostych przykładów warto spojrzeć na nie z szerszej perspektywy.

To, co uznajemy za zbiór otwarty, zależy od topologii przyjętej w danej przestrzeni.

Kluczowe jest zrozumienie, że definicja zbiorów otwartych może się zmieniać wraz z topologią.

W jednej topologii dany zbiór może być uznany za otwarty, a w innej - nie.

Innymi słowy, to topologia określa, które zbiory traktujemy jako otwarte.

Czym jest topologia? Topologia to zbiór wyróżnionych podzbiorów przestrzeni, spełniających pewne reguły: dowolna unia zbiorów otwartych jest zbiorem otwartym, a przecięcie skończonej liczby zbiorów otwartych również jest otwarte.

Z tego względu nie należy ograniczać się jedynie do znanych i intuicyjnych przykładów, takich jak przedziały czy dyski otwarte.

W topologii pojęcie „zbioru otwartego" jest znacznie szersze i obejmuje również przykłady mniej oczywiste.

Dalszy przykład

Rozważmy przestrzeń \( \{a, b\} \), złożoną tylko z dwóch punktów.

Możemy zdefiniować na niej co najmniej dwie różne topologie: trywialną i dyskretną.

• Topologia trywialna
  W topologii trywialnej jedynymi zbiorami otwartymi są \( \emptyset \) i \( \{a, b\} \). To topologia najprostsza i pozbawiona dodatkowej struktury.
• Topologia dyskretna
  W topologii dyskretnej każdy podzbiór \( \{a, b\} \) jest otwarty. Oznacza to, że \( \{a\} \), \( \{b\} \), \( \{a, b\} \) i \( \emptyset \) są zbiorami otwartymi.

Sprawdźmy teraz zbiór \( \{a\} \):

• W topologii trywialnej {a} nie jest otwarty
  Jedynym niepustym zbiorem otwartym jest tu \( \{a, b\} \).
• W topologii dyskretnej {a} jest otwarty
  Każdy podzbiór tej przestrzeni jest z definicji otwarty.

Zbiór \( \{a\} \) jest więc otwarty w topologii dyskretnej, lecz nie w topologii trywialnej.

Ten prosty przykład bardzo wyraźnie pokazuje, że pojęcie zbioru otwartego jest nierozerwalnie związane z topologią, w której pracujemy.

Twierdzenie o zbiorach otwartych

Twierdzenie 1

Niech X będzie zbiorem otwartym, a T topologią na X, tak że (X,T) tworzą przestrzeń topologiczną. Wówczas podzbiór S⊂X jest zbiorem otwartym w przestrzeni (X,T) wtedy i tylko wtedy, gdy każdy punkt s∈S posiada otoczenie U w całości zawarte w S, co oznaczamy jako U⊂S.

Z definicji S jest zbiorem otwartym, ponieważ należy do topologii (X,T).

Można zatem postrzegać S jako zbiór, w którym każdy jego punkt ma własne otoczenie wciąż pozostające w obrębie S.

Wynika z tego, że otoczenie U_s dowolnego punktu s∈S również stanowi zbiór otwarty zawarty w S.

$$ x \in U_s ⊂ S ⊂ X $$

Zbiór otwarty można traktować jako sumę otoczeń swoich punktów.

Jeżeli zatem każdy punkt s∈S posiada otoczenie U_s zawarte w S, to S musi być zbiorem otwartym, gdyż jest sumą zbiorów otwartych.

Innymi słowy, zbiór jest otwarty wtedy i tylko wtedy, gdy dla każdego jego punktu istnieje otoczenie całkowicie w nim zawarte.

Przykład. Wyobraź sobie stół pełen szklanych kulek. Każda kulka reprezentuje punkt pewnego zbioru. Powiedzieć, że zbiór jest „otwarty", to tyle, co stwierdzić, że wokół każdej kulki jest wystarczająco dużo miejsca, by mogła się poruszać, nie spadając ze stołu. Jeżeli dla każdej kulki można narysować okrąg mieszczący się w całości na powierzchni stołu (bez dotykania krawędzi), to zbiór tych kulek jest „zbiorem otwartym". Oznacza to, że niezależnie od tego, którą kulkę wybierzemy, zawsze istnieje wokół niej fragment przestrzeni, który wciąż należy do tego samego zbioru.

Twierdzenie 2

Niech \( X \) będzie zbiorem, a \( B \) - bazą topologii na \( X \). Podzbiór \( A \subset X \) jest zbiorem otwartym w topologii generowanej przez \( B \) wtedy i tylko wtedy, gdy dla każdego punktu \( x \in A \) istnieje element bazy \( B_x \) taki, że \( x \in B_x \) oraz \( B_x \subseteq A \).

Twierdzenie to podkreśla kluczową własność topologii zbudowanych przy użyciu bazy.

Innymi słowy, każdy punkt zbioru otwartego \( A \) musi mieć otoczenie \( B_x \), które pochodzi z bazy i w całości zawiera się w \( A \).

Właśnie to gwarantuje, że \( A \) jest otwarte w topologii wygenerowanej przez \( B \).

Dowód. Jeżeli A jest zbiorem otwartym w topologii generowanej przez bazę \( B \), to z definicji jest sumą elementów bazy. Oznacza to, że każdy punkt \( x \in A \) należy do pewnego zbioru bazowego \( B_x \subseteq A \). Dowód działa również w drugą stronę: jeśli każdy punkt \( x \in A \) należy do elementu bazy \( B_x \), który jest w całości zawarty w \( A \), to A - jako suma takich zbiorów - jest zbiorem otwartym.

Przykład

Rozważmy zbiór \( X = \{1, 2, 3, 4, 5\} \) oraz bazę topologii \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \). Sprawdźmy, czy \( A = \{1, 2, 3\} \) jest otwarte.

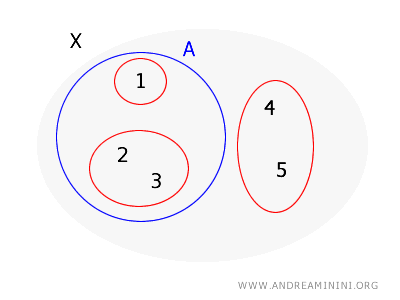
Dla każdego punktu zbioru \( A \) należy wskazać element bazy zawarty w \( A \):

• Dla punktu \( 1 \) jest to \( \{1\} \), który w całości mieści się w \( A \).
• Dla punktu \( 2 \) jest to \( \{2, 3\} \), w całości zawarty w \( A \).
• Dla punktu \( 3 \) również \( \{2, 3\} \), mieszczący się w \( A \).

Każdy punkt \( A \) jest zatem pokryty przez element bazy zawarty w \( A \), co oznacza, że \( A \) jest zbiorem otwartym w topologii generowanej przez \( B \).

Przykład 2

Ponownie rozważmy \( X = \{1, 2, 3, 4, 5\} \) i bazę \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \).

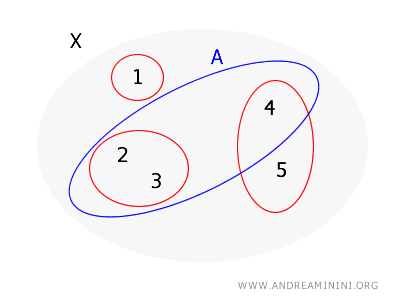
Sprawdźmy teraz, czy \( A = \{2, 3, 4\} \) jest otwarte.

• Dla punktu \( 2 \) można wskazać zbiór \( \{2, 3\} \subseteq A \).
• Dla punktu \( 3 \) otoczenie jest to samo - \( \{2, 3\} \subseteq A \).
• Dla punktu \( 4 \) nie istnieje jednak element bazy zawarty w \( A \), ponieważ jedyny element bazowy z 4 to \( \{4, 5\} \), a zawiera on 5, którego w \( A \) nie ma.

Z tego powodu \( A \) nie jest zbiorem otwartym w topologii generowanej przez \( B \), ponieważ nie każdy jego punkt posiada otoczenie pozostające w całości w \( A \).

W ten sam sposób można badać kolejne przypadki.