Homeomorfizmy w topologii

Homeomorfizm to przekształcenie topologiczne, które jest jednocześnie funkcją bijektywną i ciągłą, a jego odwrotność również zachowuje ciągłość.

W ujęciu intuicyjnym homeomorfizm pozwala przekształcić jedną przestrzeń w drugą, a następnie wrócić do stanu wyjściowego bez rozrywania ani sklejania jej części.

Inaczej mówiąc, homeomorfizm umożliwia płynne przejście między dwiema przestrzeniami przy zachowaniu ich topologicznej struktury.

Rozważmy klasyczny przykład: kubek z uchem i pączek (torus). W topologii obiekty te są homeomorficzne, ponieważ można jeden w sposób ciągły zdeformować w drugi, nie powodując przerw ani zniekształceń topologicznych.

Z perspektywy topologicznej oba kształty są równoważne, ponieważ każdy z nich ma dokładnie jeden „otwór”: w pączku jest to otwór centralny, a w kubku przestrzeń w uchu. Można więc wyobrazić sobie, że kształt kubka stopniowo przekształcamy w pączek, zachowując ciągłość powierzchni.

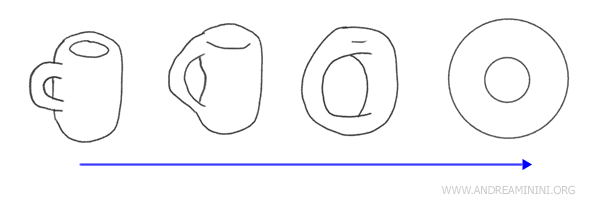
Jeśli dwie przestrzenie topologiczne są połączone homeomorfizmem, nazywamy je homeomorficznymi. Oznacza to, że z punktu widzenia topologii są one równoważne, nawet jeśli różnią się wyglądem geometrycznym.

Podstawowe własności homeomorfizmu

Oto najważniejsze cechy charakteryzujące homeomorfizm:

• Bijektywność
  Każdemu elementowi jednej przestrzeni odpowiada dokładnie jeden element drugiej i odwrotnie.
• Ciągłość
  Homeomorfizm jest z natury funkcją ciągłą: niewielkie zmiany argumentu powodują niewielkie zmiany wartości funkcji.
• Ciągłość odwrotności
  Funkcja odwrotna również musi być ciągła, co gwarantuje, że przekształcenie można odwrócić bez utraty ciągłości.
• Zachowanie własności topologicznych
  Homeomorfizm zachowuje podstawowe cechy topologiczne, takie jak ciągłość, spójność czy zwartość. W efekcie relacje między punktami przestrzeni pozostają niezmienione po przekształceniu.

Podsumowując, homeomorfizm to funkcja ciągła i bijektywna między dwiema przestrzeniami topologicznymi \(X\) i \(Y\), której odwrotność jest również ciągła. Dzięki temu obie przestrzenie mają te same własności topologiczne.

Innymi słowy, homeomorfizm pozwala przekształcić jedną przestrzeń w drugą bez rozrywania i sklejania - jest więc formą doskonałej równoważności topologicznej między strukturami przestrzennymi.

Przypomnijmy topologiczną definicję ciągłości:

Niech \(X\) i \(Y\) będą przestrzeniami topologicznymi. Funkcję \(f : X \to Y\) nazywamy ciągłą, jeśli dla każdego zbioru otwartego \(V\) w \(Y\), jego przeciwobraz \(f^{-1}(V)\) jest zbiorem otwartym w \(X\).

Innymi słowy, funkcja ciągła zachowuje strukturę zbiorów otwartych przy przejściu z jednej przestrzeni do drugiej.

Pojęcie ciągłości w topologii ma charakter bardziej abstrakcyjny i ogólny niż jego odpowiednik w analizie matematycznej.

Uwaga: W analizie ciągłość opiera się na pojęciu odległości między punktami, natomiast w topologii - wyłącznie na strukturze zbiorów otwartych, bez odniesienia do metryki.

Przykład

Aby lepiej zilustrować pojęcie ciągłości i homeomorfizmu, przyjrzyjmy się prostemu przykładowi z użyciem zbiorów otwartych.

Niech \(X = \{a, b, c, d\}\) i \(Y = \{1, 2\}\) będą przestrzeniami topologicznymi.

• W \(X\) zbiorami otwartymi są: \(\{\}, \{a\}, \{a, b\}, \{a, b, c, d\}\).
• W \(Y\) zbiorami otwartymi są: \(\{\}, \{1\}, \{1, 2\}\).

Funkcja \(f : X \to Y\) jest ciągła, jeśli przeciwobraz każdego zbioru otwartego w \(Y\) jest zbiorem otwartym w \(X\).

Zdefiniujmy funkcję \(f\) następująco:

\(f(a) = 1\), \(f(b) = 1\), \(f(c) = 2\), \(f(d) = 2\).

Dla większej przejrzystości przedstawmy przestrzenie i działanie funkcji \(f\), oznaczając zbiory otwarte okręgami.

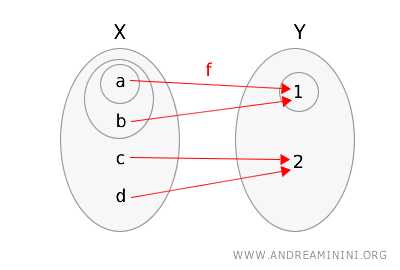
Sprawdźmy definicję ciągłości:

• Dla zbioru otwartego \(\{1\}\) w \(Y\), przeciwobraz to \(f^{-1}(\{1\}) = \{a, b\}\), który jest otwarty w \(X\).
• Dla zbioru \(\{1, 2\}\) w \(Y\), przeciwobraz to \(f^{-1}(\{1, 2\}) = \{a, b, c, d\}\), również otwarty w \(X\).

Skoro przeciwobraz każdego zbioru otwartego w \(Y\) jest otwarty w \(X\), funkcja \(f\) jest ciągła.

Uwaga: Zbiór pusty pomijamy, ponieważ z definicji jest otwarty w każdej przestrzeni topologicznej.

Rozważmy teraz inną funkcję \(g : X \to Y\), określoną przez:

\(g(a) = 1\), \(g(b) = 1\), \(g(c) = 1\), \(g(d) = 2\).

Przedstawmy ją graficznie, zaznaczając odpowiednie zbiory otwarte.

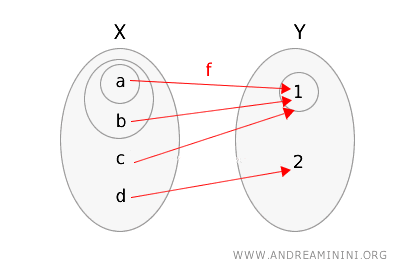
Sprawdzenie ciągłości:

• Zbiór otwarty \(\{1\}\) w \(Y\) ma przeciwobraz \(g^{-1}(\{1\}) = \{a, b, c\}\), który nie jest otwarty w \(X\).

Skoro istnieje zbiór otwarty w \(Y\), którego przeciwobraz nie jest otwarty w \(X\), funkcja \(g\) nie jest ciągła.

Uwaga: Funkcja jest ciągła wtedy i tylko wtedy, gdy przeciwobraz każdego zbioru otwartego w przestrzeni docelowej (\(Y\)) jest zbiorem otwartym w przestrzeni wyjściowej (\(X\)). W pierwszym przypadku funkcja \(f\) spełnia ten warunek, w drugim - \(g\) już nie.

Definicja homeomorfizmu

Niech \(X\) i \(Y\) będą przestrzeniami topologicznymi, a \(f : X \to Y\) funkcją bijektywną z odwrotnością \(f^{-1} : Y \to X\). Jeśli zarówno \(f\), jak i \(f^{-1}\) są ciągłe, to \(f\) nazywamy homeomorfizmem, a przestrzenie \(X\) i \(Y\) są homeomorficzne, co zapisujemy \(X \cong Y\).

Takie przestrzenie nazywamy również równoważnymi topologicznie.

Co to oznacza w praktyce?

Dwie przestrzenie są homeomorficzne (czyli topologicznie równoważne), gdy mają identyczną strukturę topologiczną, nawet jeśli ich kształty geometryczne różnią się znacząco.

Homeomorfizm spełnia trzy zasadnicze warunki:

1. Bijektywność - funkcja \(f : X \to Y\) jest jednocześnie różnowartościowa i „na”, co oznacza, że każdemu punktowi z \(X\) odpowiada dokładnie jeden punkt z \(Y\) i odwrotnie.
2. Ciągłość funkcji \(f\) - funkcja jest ciągła, jeśli przeciwobraz każdego zbioru otwartego w \(Y\) jest otwarty w \(X\).
3. Ciągłość funkcji odwrotnej \(f^{-1}\) - funkcja odwrotna \(f^{-1} : Y \to X\) również musi być ciągła, czyli przeciwobraz każdego zbioru otwartego w \(X\) jest otwarty w \(Y\).

Przykład: Wyobraźmy sobie kartkę papieru zwiniętą w cylinder. Cylinder i płaska kartka są homeomorficzne, ponieważ można przejść od jednej do drugiej bez cięcia i klejenia - wystarczy zwijać lub rozwijać. Choć ich kształty geometryczne różnią się, struktura topologiczna (czyli zbiory otwarte) pozostaje identyczna.

Warto zauważyć, że sama ciągłość funkcji bijektywnej \(f\) nie gwarantuje ciągłości jej odwrotności \(f^{-1}\), chyba że \(f\) jest funkcją otwartą.

Innymi słowy, funkcja ciągła i bijektywna nie musi być homeomorfizmem, jeśli jej odwrotność nie jest ciągła.

W topologii mówimy, że funkcja \(f : X \to Y\) jest ciągła, gdy przeciwobraz każdego zbioru otwartego w \(Y\) jest otwarty w \(X\).

Nie wynika z tego jednak, że obraz zbioru otwartego w \(X\) musi być otwarty w \(Y\).

Aby \(f^{-1}\) była ciągła, funkcja \(f\) musi być nie tylko ciągła i bijektywna, lecz także funkcją otwartą.

Przykład

Rozważmy następujące przestrzenie topologiczne:

• \( X = (a, b) \) z topologią \( T_X = \{\emptyset, \{a\}, \{b\}, X\} \).
• \( Y = (1, 2) \) z topologią \( T_Y = \{\emptyset, Y\} \).

Zdefiniujmy odwzorowanie \( f : X \to Y \), określone wzorem \( f(a) = 1 \), \( f(b) = 2 \).

Odwzorowanie \( f \) jest oczywiście bijektywne - każdy element zbioru \( X \) ma dokładnie jeden odpowiednik w \( Y \), i odwrotnie.

Uwaga: Na ilustracji zbiory otwarte oznaczono okręgami. W przestrzeni \( X \) zbiory \{a\}, \{b\} oraz \{a, b\} są otwarte, natomiast w \( Y \) jedynym niepustym zbiorem otwartym jest \{1, 2\}. Zbiorów pustych - z definicji otwartych - nie uwzględniono na rysunku.

Przeanalizujmy teraz ciągłość funkcji \( f \) oraz jej odwrotności \( f^{-1} \).

• Ciągłość funkcji \( f \)
  Topologia \( T_Y \) zawiera jedynie \( \emptyset \) i \( Y \). Otrzymujemy:
  • \( f^{-1}(\emptyset) = \emptyset \), które jest otwarte w \( T_X \)
  • \( f^{-1}(Y) = X \), również otwarte w \( T_X \)
  Zatem \( f \) jest funkcją ciągłą.
• Ciągłość funkcji odwrotnej \( f^{-1} \)
  Rozważmy teraz odwrotność \( f^{-1} : Y \to X \), gdzie \( f^{-1}(1) = a \) oraz \( f^{-1}(2) = b \). Dla zbiorów otwartych w \( X \) mamy:
  • \( f^{-1}(\emptyset) = \emptyset \), otwarty w \( T_Y \)
  • \( f^{-1}(\{a\}) = \{1\} \), który nie jest otwarty w \( T_Y \)
  • \( f^{-1}(\{b\}) = \{2\} \), również nieotwarty
  • \( f^{-1}(X) = Y \), otwarty w \( T_Y \)
  Ponieważ nie wszystkie przeciwobrazy są otwarte, funkcja \( f^{-1} \) nie jest ciągła.

Wniosek: mimo że funkcja \( f \) jest bijektywna i ciągła, jej odwrotność nie jest ciągła. Zatem \( f \) nie jest homeomorfizmem.

Przykład ten pokazuje, że sama ciągłość i bijektywność odwzorowania nie gwarantują ciągłości odwrotności.

Uwaga: Brak ciągłości odwrotności wynika z różnicy w „ziarnistości" topologii - topologia \( T_X \) jest drobniejsza (bogatsza w zbiory otwarte) niż \( T_Y \), która jest grubszą topologią.

Przykład 2

Rozważmy teraz inny przypadek z odmiennym doborem topologii:

• \( X = (a, b) \) z topologią \( T_X = \{\emptyset, \{a\}, X\} \).
• \( Y = (1, 2) \) z topologią \( T_Y = \{\emptyset, \{1\}, Y\} \).

Zdefiniujmy funkcję \( f : X \to Y \) poprzez \( f(a) = 1 \) oraz \( f(b) = 2 \).

Odwzorowanie \( f \) jest ponownie bijektywne.

Sprawdźmy teraz, czy \( f \) oraz \( f^{-1} \) są ciągłe.

• Ciągłość funkcji \( f \)
  W \( Y \) zbiory otwarte to \( \emptyset \), \(\{1\}\) oraz \( Y \):
  • \( f^{-1}(\emptyset) = \emptyset \), otwarty w \( T_X \)
  • \( f^{-1}(\{1\}) = \{a\} \), otwarty w \( T_X \)
  • \( f^{-1}(Y) = X \), również otwarty w \( T_X \)
  Wszystkie przeciwobrazy są otwarte, więc \( f \) jest ciągła.
• Ciągłość odwrotności \( f^{-1} \)
  W \( X \) zbiory otwarte to \( \emptyset \), \(\{a\}\) oraz \( X \):
  • \( f^{-1}(\emptyset) = \emptyset \), otwarty w \( T_Y \)
  • \( f^{-1}(\{a\}) = \{1\} \), otwarty w \( T_Y \)
  • \( f^{-1}(X) = Y \), również otwarty w \( T_Y \)
  Odwrotność \( f^{-1} \) jest więc również funkcją ciągłą.

Otrzymujemy zatem, że \( f \) jest bijektywna, ciągła, a jej odwrotność również. W konsekwencji \( f \) jest homeomorfizmem.

Różnica względem pierwszego przykładu polega na tym, że tym razem dobrane topologie są ze sobą zgodne - w obu przestrzeniach mają podobną strukturę otwartych zbiorów.

Uwaga: Ten przykład pokazuje, że aby odwrotność funkcji była ciągła, a więc by istniał homeomorfizm, konieczne jest dobranie kompatybilnych topologii w przestrzeniach \( X \) i \( Y \).

Różnice między homeomorfizmami a innymi przekształceniami topologicznymi

Choć termin „homeomorfizm" bywa potocznie używany jako synonim przekształceń topologicznych, w ścisłym znaczeniu odnosi się on do szczególnego typu takich przekształceń.

Homeomorfizmy i ogólne przekształcenia topologiczne są ze sobą ściśle powiązane, ale nie oznaczają dokładnie tego samego:

• Przekształcenia topologiczne
  Obejmują szeroką klasę odwzorowań między przestrzeniami topologicznymi, które zachowują pewne kluczowe własności, takie jak ciągłość, spójność czy zwartość. Do tej kategorii należą homeomorfizmy, ale również inne formy przekształceń, m.in. izotopie, homotopie oraz dyfeomorfizmy.
• Homeomorfizmy
  Są to odwzorowania bijektywne i ciągłe, których odwrotność również jest ciągła. Ustanawiają one pełną zgodność topologiczną między dwiema przestrzeniami, zachowując ich wewnętrzną strukturę. Dwie przestrzenie połączone homeomorfizmem są zatem topologicznie równoważne, mimo że mogą różnić się kształtem geometrycznym.

Podsumowując, każdy homeomorfizm jest przekształceniem topologicznym, lecz nie każde przekształcenie topologiczne jest homeomorfizmem.

Niektóre odwzorowania, mimo że zachowują kluczowe własności topologiczne, nie spełniają wszystkich warunków definicji homeomorfizmu.

Dodatkowe uwagi

Poniżej przedstawiono kilka uzupełniających spostrzeżeń, które pomagają lepiej zrozumieć znaczenie i konsekwencje pojęcia homeomorfizmu:

• Własność topologiczna
  To cecha przestrzeni, która pozostaje niezmieniona przy homeomorfizmach. Innymi słowy, jeśli dwie przestrzenie są homeomorficzne (połączone odwzorowaniem ciągłym, bijektywnym i z ciągłą odwrotnością), to mają dokładnie te same własności topologiczne.
• Twierdzenie Hausdorffa o homeomorfizmach
  Twierdzenie to głosi, że jeśli \( f : X \to Y \) jest homeomorfizmem, a \( X \) jest przestrzenią Hausdorffa, to \( Y \) również nią jest. Ponieważ homeomorfizmy zachowują własności topologiczne, również cecha rozdzielania punktów typowa dla przestrzeni Hausdorffa przenosi się z \( X \) na \( Y \).
• Odpowiednikiem homeomorfizmu w algebrze jest izomorfizm grup. Podczas gdy izomorfizm zachowuje strukturę algebraiczną, homeomorfizm zachowuje strukturę topologiczną - czyli organizację zbiorów otwartych w przestrzeni.

I tak dalej.