Przestrzeń Hausdorffa

Przestrzeń Hausdorffa to taka przestrzeń topologiczna, w której dowolne dwa różne punkty można wyraźnie oddzielić za pomocą rozłącznych otoczeń otwartych. W praktyce oznacza to, że każdy punkt ma swoje własne „miejsce” w przestrzeni, tak wyraźnie zarysowane, że nie da się go pomylić z innymi.

Mówiąc prościej: jeśli $ x \ne y $, to istnieją zbiory otwarte $ U $ i $ V $, które zawierają odpowiednio $ x $ i $ y $, a jednocześnie nie mają części wspólnej.

To intuicyjne podejście do rozdzielania punktów jest fundamentem wielu zagadnień analizy i geometrii. Dzięki warunkowi Hausdorffa pojęcia takie jak zbieżność i granica nabierają przejrzystości - a same granice okazują się jednoznaczne.

Warto też pamiętać, że w każdej przestrzeni Hausdorffa singletony, czyli zbiory zawierające dokładnie jeden punkt, są zbiorami domkniętymi. Wynika to z faktu, że ich dopełnienia są otwarte.

Przykłady
Uwagi końcowe

Przykłady

Przykład 1: prosta rzeczywista

Weźmy dobrze znaną topologię standardową na $\mathbb{R}$, opartą na przedziałach otwartych.

schemat prostej rzeczywistej

W tej topologii singleton $ \{x\} $ nie jest otwarty, ponieważ nie może zawierać żadnego otwartego sąsiedztwa. Każde takie sąsiedztwo w $\mathbb{R}$ jest zbiorem o nieskończonej liczbie punktów, więc nie mieści się w singletonie.

Z kolei jego dopełnienie, czyli $ \mathbb{R} \setminus \{x\} $, jest otwarte. To prowadzi do wniosku, że singleton jest domknięty.

otwarte sąsiedztwo singletonu

Dodatkowo, prosta rzeczywista jest przestrzenią Hausdorffa. Jeśli $ a \ne b $, zawsze znajdziemy dwa otwarte przedziały rozłączne, które oddzielają te punkty.

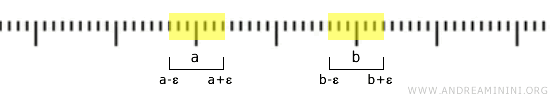
otoczenia punktów a i b

Jeżeli $ a < b $, wystarczy wybrać $ \varepsilon > 0 $ tak, by $ a + \varepsilon < b - \varepsilon $. Wtedy przedziały $ (a - \varepsilon, a + \varepsilon) $ i $ (b - \varepsilon, b + \varepsilon) $ są od siebie oddzielone.

To klasyczny przykład przestrzeni spełniającej warunek Hausdorffa.

Przykład 2: topologia dyskretna

Rozważmy przestrzeń $ X = \{1, 2, 3\} $ wyposażoną w topologię dyskretną.

W topologii dyskretnej każdy podzbiór jest otwarty. W szczególności dotyczy to singletonów.

zbiór pusty $ \emptyset $
singletony $ \{1\}, \{2\}, \{3\} $
podzbiory dwuelementowe $ \{1, 2\}, \{1, 3\}, \{2, 3\} $
zbiór pełny $ \{1, 2, 3\} $

Łącznie daje to $ 2^3 = 8 $ otwartych zbiorów - dokładnie wszystkie podzbiory przestrzeni.

W takiej przestrzeni każdą parę punktów można bez trudu oddzielić. Dla $ x \ne y $ wystarczy wziąć otwarte zbiory $ \{x\} $ i $ \{y\} $.

Na przykład:

$$ \{1\} \cap \{2\} = \emptyset $$

Czy singletony są tutaj otwarte czy domknięte?

Odpowiedź brzmi: jednym i drugim. W topologii dyskretnej singletony są klopen - jednocześnie otwarte i domknięte. Wynika to z faktu, że ich dopełnienia są również otwarte, a więc spełniają definicję zbiorów domkniętych.

Przykład: w $ X = \{1, 2, 3\} $, zbiór $ \{1\} $ jest otwarty, a jego dopełnienie $ \{2, 3\} $ także jest otwarte. Dlatego $ \{1\} $ jest jednocześnie domknięty.

Różnica między topologią dyskretną a standardową polega na tym, że w topologii standardowej tylko niektóre podzbiory spełniają warunek otwartości, natomiast w dyskretnej - wszystkie bez wyjątku.

Uwagi końcowe

Jedną z najważniejszych konsekwencji warunku Hausdorffa jest jednoznaczność granic.

W każdej przestrzeni Hausdorffa ciąg zbieżny ma dokładnie jedną granicę.

Dla ciągu zbieżnego nie można wskazać dwóch różnych punktów, do których miałby on jednocześnie dążyć. Gdyby tak było, można by te punkty oddzielić rozłącznymi otoczeniami, co przeczyłoby pojęciu zbieżności.

Dowód w skrócie: Jeśli ciąg $ x_n $ zbiega do punktu $ x $, to od pewnego miejsca wszystkie jego wyrazy należą do każdego otwartego otoczenia $ U $ punktu $ x $. Jeśli rzekomo miałby także zbiegać do innego punktu $ y \ne x $, to od pewnego miejsca musiałby jednocześnie znajdować się w otoczeniach $ U $ i $ V $ tych dwóch punktów. W przestrzeni Hausdorffa otoczenia te są rozłączne, więc taka sytuacja jest niemożliwa.

Wniosek jest prosty: w przestrzeni Hausdorffa granice są zawsze jednoznaczne. Dzięki temu teoria zbieżności jest przejrzysta i stabilna, co czyni te przestrzenie fundamentalnymi w wielu działach matematyki.