Przestrzenie regularne w topologii
Przestrzeń topologiczną \( X \) nazywamy regularną, jeśli spełnia dwa podstawowe warunki:
- Każdy punkt tworzy zbiór domknięty. Oznacza to, że jednopunktowe zbiory są w niej automatycznie domknięte.
- Punkt można oddzielić od zbioru domkniętego. Dla dowolnego punktu \( a \in X \) oraz zbioru domkniętego \( C \subset X \), który nie zawiera \( a \), istnieją dwa otwarte, rozłączne zbiory \( U \) i \( V \) takie, że: \[ a \in U,\quad C \subset V,\quad U \cap V = \emptyset. \]
Regularność to jedna z kluczowych własności oddzielania w topologii. W porównaniu z przestrzeniami Hausdorffa daje silniejszą kontrolę nad tym, jak rozróżniać elementy przestrzeni, choć same pojęcia nie są równoważne.
Co więcej, jeśli przestrzeń regularna ma przeliczalną bazę, wówczas zgodnie z twierdzeniem Urysohna okazuje się metryzowalna, czyli można wprowadzić na niej metrykę zgodną z jej topologią.
Czym dokładnie różni się regularność od warunku Hausdorffa?
W przestrzeni Hausdorffa możemy oddzielić dwa różne punkty. W przestrzeni regularnej idziemy krok dalej: potrafimy oddzielić punkt od dowolnego zbioru domkniętego, który go nie zawiera. To subtelne, ale bardzo istotne wzmocnienie, szczególnie w analizie struktur bardziej złożonych niż zwykłe zbiory punktów.
Uwaga. Przestrzeń regularna nie jest automatycznie normalna. Normalność wymaga możliwości oddzielania dowolnych dwóch rozłącznych zbiorów domkniętych. Każda przestrzeń normalna jest regularna, lecz nie każda regularna spełnia warunek normalności.
Warto też pamiętać, że regularność to tylko jeden z wielu aksjomatów oddzielania. Istnieją przestrzenie regularne, które nie są Hausdorffa, oraz przestrzenie Hausdorffa, które nie są regularne. Topologia tworzy tu ciekawą sieć zależności, a nie prostą hierarchię.
Przykład ilustrujący regularność
Najbardziej naturalnym przykładem przestrzeni regularnej jest prosta rzeczywista \( \mathbb{R} \) z topologią standardową.
Weźmy punkt \( x = 2 \) oraz zbiór domknięty:
\[ C = (-\infty, 0] \cup [5, \infty). \]
Punkt 2 nie należy do \( C \), a sam zbiór jest domknięty w zwykłej topologii.

Chcemy teraz znaleźć dwa zbiory otwarte, które oddzielą punkt \( x \) od zbioru \( C \). Zwróćmy uwagę, że dopełnienie \( C \) jest otwarte, a przedział \( (0, 5) \) zawiera interesujący nas punkt:
\[ (a, b) = (0, 5). \]
Wybierzmy liczby:
\[ 0 < c < 2 < d < 5, \]
na przykład \( c = 1 \) i \( d = 3 \).
Zbudujmy teraz dwa otwarte zbiory:
- \( U = (1, 3) \), zawierający punkt \( x = 2 \).
- \( V = (-\infty, 1) \cup (3, \infty) \), obejmujący cały zbiór \( C \).
Zbiory \( U \) i \( V \) są rozłączne, co daje dokładnie taką separację, jakiej wymaga definicja regularności.
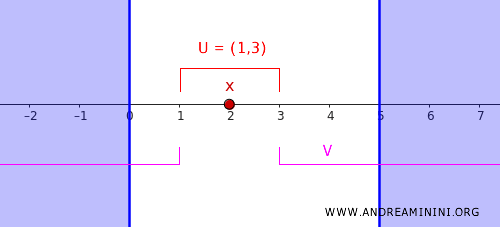
To proste ćwiczenie na prostej liczbowej dobrze pokazuje, na czym polega regularność, zanim przejdziemy do bardziej abstrakcyjnych przykładów.
Uwagi końcowe
Aby lepiej zrozumieć regularność, warto spojrzeć na nią w szerszym kontekście aksjomatów oddzielania. Opisują one precyzję topologii, czyli to, jak skutecznie możemy odróżniać punkty i podzbiory, korzystając z otoczeń otwartych.
- Aksjomaty oddzielania
Pojęcia takie jak Hausdorff, regularność czy normalność określają różne poziomy „dokładności" topologii.Uwaga. W przestrzeni Hausdorffa różne punkty mają rozłączne otwarte otoczenia. W przestrzeni regularnej oddzielić można także punkt od rozłącznego zbioru domkniętego. To dobre porównanie do jakości obrazu: im wyższa rozdzielczość, tym więcej szczegółów można dostrzec.
W kolejnych częściach można przejść do bardziej złożonych przykładów oraz do powiązań regularności z innymi własnościami topologicznymi.