Kula otwarta

W topologii kula otwarta - nazywana także otwartym otoczeniem kołowym, dyskiem lub otwartą sferą - to zbiór wszystkich punktów, które znajdują się w odległości ściśle mniejszej niż pewien promień \( r \) od środka \( c \). Definicję zapisujemy następująco: $$ B(c, r) = \{ x \in M \mid d(c, x) < r \} $$

Pojęcie to należy do teorii przestrzeni metrycznych \( M \), w których metryka \( d \) wyznacza odległość między punktami. To właśnie metryka decyduje o tym, jak wygląda lokalna geometria i struktura danej przestrzeni.

Kula otwarta jest w pełni określona przez dwie informacje: jej środek oraz promień.

Mówimy, że jest „otwarta", ponieważ każdy punkt znajdujący się w jej wnętrzu ma własną, mniejszą kulę całkowicie zawartą w kuli pierwotnej. Ta lokalna własność jest fundamentem wielu pojęć topologii.

Uwaga: Kule otwarte są niezmiennicze względem translacji i homotetii. Ich przesunięcie lub jednolite przeskalowanie nie zmienia żadnej z ich cech topologicznych.

Rozważmy płaszczyznę \( \mathbb{R}^2 \). Odległość pomiędzy punktem \( p = (x, y) \) a środkiem \( c = (x_0, y_0) \) opisuje klasyczna metryka euklidesowa:

$$ d(p,c) = \sqrt{(x - x_0)^2 + (y - y_0)^2} $$

Kule otwarte są podstawowym elementem budowania topologii w przestrzeniach metrycznych. W przypadku \( \mathbb{R}^2 \) tworzą one bazę standardowej topologii euklidesowej, czyli tej, która odpowiada naszemu intuicyjnemu pojęciu „ciągłości".

Rodzina kul otwartych o dowolnych środkach i dodatnich promieniach opisuje tę topologię w pełni:

$$ B = \{ B(p, r) \ | \ p \in \mathbb{R}^2,\ r > 0 \} $$

Wśród wielu topologii, które można wprowadzić na \( \mathbb{R}^2 \), ta oparta na euklidesowych kulach otwartych pozostaje najbardziej naturalna i jest standardem w analizie i topologii.

Co ważne, w każdej kuli otwartej \( B(p,r) \) dowolny punkt \( q \in B(p,r) \) może być środkiem mniejszej kuli \( B(q,\epsilon) \), która w całości mieści się w kuli wyjściowej.

Ta kluczowa własność przyjmuje postać formalną:

$$ \forall\ q \in B(p,r),\ \exists\ \epsilon > 0\ \text{takie, że}\ B(q,\epsilon) \subset B(p,r) $$

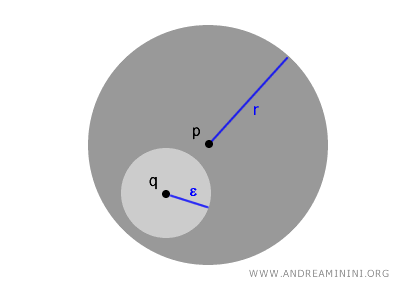
Możliwość powtarzania tego procesu w nieskończoność pokazuje, jak bardzo lokalny charakter mają kule otwarte i jak fundamentalną rolę odgrywają w opisie struktury przestrzeni topologicznych.