Normalna przestrzeń topologiczna
Przestrzeń topologiczną \( X \) nazywamy normalną, jeżeli spełnia dwa fundamentalne warunki separacyjne:
- Singletony są domknięte
Dla każdego punktu \( x \in X \) zbiór jednoelementowy \(\{x\}\) jest domknięty w danej topologii. - Rozłączne zbiory domknięte można oddzielić rozłącznymi zbiorami otwartymi
Jeśli \( A \cap B = \emptyset \), to istnieją takie otwarte zbiory \( U \) i \( V \), że:
- \( A \subset U \),
- \( B \subset V \),
- \( U \cap V = \emptyset \).
Normalność jest jedną z kluczowych własności separacyjnych w topologii. Intuicyjnie mówi nam, że jeśli dwa zbiory domknięte nie mają punktów wspólnych, to przestrzeń jest na tyle „dobrze ułożona”, że możemy otoczyć każdy z nich osobnym zbiorem otwartym i te otwarte obszary również nie będą się przecinać. Taka możliwość leży u podstaw wielu ważnych konstrukcji, zwłaszcza funkcji ciągłych, które pozwalają rozróżniać punkty oraz zbiory.
Przykład
Przyjrzyjmy się standardowej przestrzeni topologicznej \( \mathbb{R} \), gdzie otwarte zbiory to przedziały postaci \( (a, b) \).
Rozważmy dwa rozłączne zbiory domknięte:
- \( A = \{0\} \), czyli pojedynczy punkt,
- \( B = [2, 3] \), klasyczny przedział domknięty.
Oba są domknięte, a ponieważ nie mają wspólnych elementów, są również rozłączne.
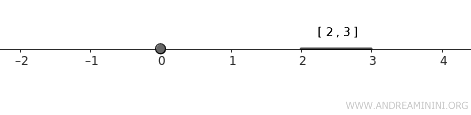
Uwaga. Singleton \( A \) jest domknięty jako zbiór jednoelementowy. Przedział \( B \) także jest zbiorem domkniętym, zgodnie z definicją.
Aby je odseparować, wystarczy dobrać właściwe otoczenia otwarte.
Dla \( A \) naturalnym kandydatem jest przedział otwarty \( U = (-1, 1) \), obejmujący punkt \( 0 \).
$$ A \subset U = (-1,1) $$
Dla \( B \) wybieramy przedział \( V = (1, 4) \), który obejmuje cały \( [2,3] \).
$$ B \subset V = (1,4) $$
Zwróć uwagę, że zbiory \( U \) i \( V \) w ogóle się nie przecinają. Spełniają więc dokładnie to, czego wymaga definicja normalności.
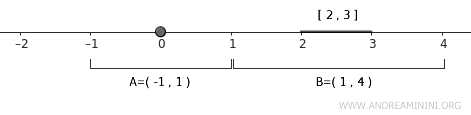
Ta sama metoda działa w każdym przypadku: jeśli dwa zbiory domknięte w \( \mathbb{R} \) są rozłączne, można zawsze znaleźć otwarte otoczenia, które je jednoznacznie rozdzielą. To właśnie czyni prostą rzeczywistą dobrym przykładem przestrzeni normalnej.
Dodatkowe uwagi
Poniżej kilka faktów, które porządkują miejsce przestrzeni normalnych w topologii:
- \( \mathbb{R} \) ze standardową topologią jest przestrzenią normalną
Spełnia zarówno warunek regularności, jak i silniejszy warunek normalności. - Każda przestrzeń metryczna jest normalna
Metryka zapewnia automatycznie wszystkie własności potrzebne do normalności. - Normalność pociąga za sobą regularność
Jeśli przestrzeń jest normalna, jest również regularna, chociaż odwrotność nie musi zachodzić.
Normalne przestrzenie topologiczne stanowią fundament wielu klasycznych twierdzeń separacyjnych. Pozwalają porządkować strukturę przestrzeni i zapewniają narzędzia niezbędne do analizy ciągłości, metryzowalności oraz rozszerzania funkcji.