Przekształcenia topologiczne - jak zmieniać kształt bez rozrywania

Przekształcenia topologiczne to takie deformacje przestrzeni, które zachowują jej podstawowe własności - ciągłość, spójność i sposób połączenia elementów. Innymi słowy, topologia nie interesuje się dokładnymi wymiarami, lecz tym, co pozostaje niezmienne mimo dowolnego rozciągania, wyginania czy skręcania obiektów.

To właśnie dzięki takim przekształceniom możemy powiedzieć, że w sensie topologicznym pączek i filiżanka to ten sam obiekt - oba mają jeden otwór. Fascynujące, prawda?

Na czym polegają przekształcenia topologiczne?

W topologii chodzi o badanie własności, które nie zmieniają się przy ciągłych deformacjach. Tego typu przekształcenia mają kilka kluczowych cech:

• Ciągłość
  Małe zmiany na wejściu powodują małe zmiany na wyjściu - bez skoków i przerw. To podstawowa zasada, dzięki której obiekt „pozostaje sobą" mimo deformacji.
• Spójność
  Punkty, które były połączone lub blisko siebie w oryginalnej przestrzeni, pozostają takimi również po przekształceniu. Spójność to serce topologii.
• Bez rozrywania i sklejania
  Można zginać, ściskać i rozciągać, ale nie wolno rozrywać ani sklejać. To właśnie odróżnia przekształcenie topologiczne od zwykłej zmiany kształtu.

W praktyce: takie przekształcenia mają zastosowanie w wielu dziedzinach - od teorii węzłów i topologii algebraicznej po analizę struktur sieci i kształtów w grafice komputerowej.

Rodzaje przekształceń topologicznych

Topologia wyróżnia kilka typów przekształceń, z których każde opisuje inny sposób zachowania ciągłości i struktury przestrzeni:

• Homeomorfizmy
  To odwzorowania ciągłe z ciągłym odwzorowaniem odwrotnym. Umożliwiają przejście z jednej przestrzeni do drugiej i z powrotem bez rozrywania. Klasyczny przykład? Filiżanka i pączek - dwa obiekty homeomorficzne.
• Izotopie
  To płynne przekształcenia, w których każdy etap jest sam w sobie homeomorfizmem. Wyobraź sobie powolne przesuwanie węzła na linie - w każdym momencie węzeł zachowuje ciągłość.
• Homotopie
  Pokazują, jak można płynnie przeobrazić jedną funkcję w drugą, nie tracąc ciągłości. Przykład? Rozciąganie i kurczenie sprężyny - każdy etap tego ruchu to homotopia.
• Dyfeomorfizmy
  To homeomorfizmy, które są dodatkowo gładkie i różniczkowalne. Odgrywają kluczową rolę w topologii różniczkowej, gdzie liczy się nie tylko ciągłość, ale też „gładkość" powierzchni, np. gdy kula zmienia się w elipsoid.

Geometria kontra topologia

Na pierwszy rzut oka geometria i topologia wydają się podobne - obie opisują przestrzeń. Różnią się jednak tym, co uważają za istotne:

• Przekształcenia geometryczne
  Zachowują odległości, kąty i proporcje. Obejmują translacje, obroty, odbicia i skalowania.

  Przykład: obrót figury zmienia jej położenie, ale nie jej kształt.

• Przekształcenia topologiczne
  Zachowują ciągłość i spójność, ale nie dbają o długości i kąty. Dzięki temu pozwalają na niezwykłą elastyczność - można zginać i deformować bez ograniczeń.

  Przykład: pączek można „przekształcić" w filiżankę, bo oba mają jeden otwór.

Krótko mówiąc: geometria bada to, jak coś wygląda, a topologia - czy pozostaje połączone.

Czy przekształcenie może być jednocześnie geometryczne i topologiczne?

Tak! Niektóre przekształcenia spełniają oba warunki - są jednocześnie geometryczne i topologiczne. Dzieje się tak, gdy zachowują zarówno kształt i proporcje, jak i ciągłość przestrzeni.

• Izometrie
  Translacje, obroty i odbicia nie zmieniają odległości ani kątów, a przy tym są ciągłe i odwracalne. To idealny przykład przekształceń, które łączą oba światy.
  
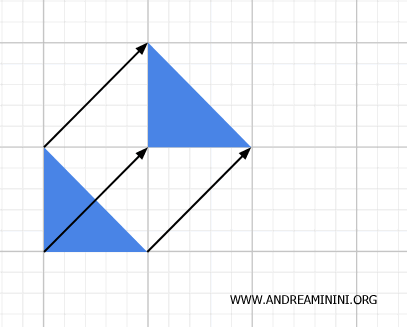
• Podobieństwa
  Zmieniają skalę obiektu, ale zachowują jego kształt i proporcje. Choć powiększają lub pomniejszają, nie naruszają spójności - dlatego również są jednocześnie geometryczne i topologiczne.

Topologia pokazuje, że świat form jest bardziej elastyczny, niż się wydaje. Wystarczy spojrzeć na rzeczywistość nie przez pryzmat miary i kąta, lecz przez ciągłość i połączenia - a wtedy filiżanka naprawdę staje się pączkiem.