Standardowa topologia na prostej rzeczywistej

Standardowa (zwyczajna) topologia na \( \mathbb{R} \) to najbardziej podstawowy i intuicyjny sposób opisu zbiorów otwartych. Jest ona zbudowana na przedziałach otwartych \( (a, b) \), gdzie \( a < b \), oraz na wszystkich ich sumach - zarówno skończonych, jak i nieskończonych. Każdy taki zbiór traktujemy jako zbiór otwarty.

Formalnie, zbiór \( U \subseteq \mathbb{R} \) jest otwarty, jeśli dla każdego punktu \( x \in U \) istnieje przedział otwarty \( (a, b) \) taki, że \( x \in (a, b) \) i \( (a, b) \subseteq U \).

$$ x \in (a,b) \subseteq U $$

Innymi słowy, każdy punkt \( x \) należący do zbioru otwartego \( U \) ma swoje otoczenie w postaci przedziału otwartego, które w całości mieści się w \( U \).

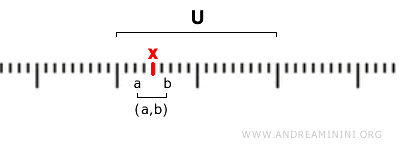
W standardowej topologii za otwarte uznaje się przede wszystkim:

• Przedziały otwarte
  Wszystkie zbiory otwarte w tej topologii to przedziały \( (a, b) \) z \( a < b \), a także dowolne ich sumy. W ten sposób można opisać każdy otwarty fragment prostej rzeczywistej.
• Operacje na zbiorach otwartych
  Standardowa topologia zachowuje swoje własności przy podstawowych operacjach na zbiorach:
  • Suma: Dowolna suma (skończona lub nieskończona) zbiorów otwartych jest również zbiorem otwartym.
  • Skończone przecięcia: Przecięcie skończonej liczby zbiorów otwartych również daje zbiór otwarty.

Standardowa topologia to tylko jeden z wielu możliwych układów topologicznych na zbiorze \( X \). Nazywamy ją „standardową”, ponieważ jest najczęściej stosowana i stanowi punkt odniesienia dla większości innych topologii. Jej siła polega na tym, że w naturalny sposób oddaje intuicyjne pojęcia takie jak bliskość, otwartość i ciągłość - szczególnie na prostej rzeczywistej \( \mathbb{R} \).

Uwaga: Na \( \mathbb{R} \) i innych przestrzeniach można zdefiniować także inne topologie, oparte na różnych bazach topologicznych. Używa się ich, gdy chcemy badać szczególne własności lub opisywać przestrzenie matematyczne z innego punktu widzenia.

Przykład praktyczny

Podstawą standardowej topologii na \( \mathbb{R} \) jest zbiór wszystkich przedziałów otwartych \( (a, b) \), dla których \( a < b \):

$$ B = \{ (a,b) \subset \mathbb{R} \ | \ a<b \} $$

Dla każdego punktu \( x \in U \), gdzie \( U \) jest zbiorem otwartym, istnieje pewne \( \epsilon>0 \) takie, że przedział \( (x-\epsilon, x+\epsilon) \) mieści się w \( U \). Spełnia to definicję zbioru otwartego w topologii standardowej.

$$ \forall \ x \in U \ \exists \ \epsilon>0 \ | \ (x-\epsilon, x+\epsilon) \subseteq U $$

Tę topologię nazywamy „standardową”, ponieważ to właśnie ona leży u podstaw ścisłych definicji pojęć takich jak ciągłość funkcji czy granica ciągu liczbowego.

Przykład 2

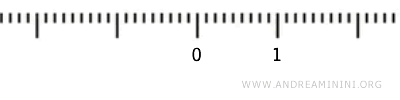
Rozważmy przedział \( (0,1) \), który nie zawiera swoich końców \( 0 \) i \( 1 \). Zastanówmy się, jak wygląda jego struktura topologiczna w kontekście topologii standardowej.

W topologii indukowanej podzbiór \( U \subset (0,1) \) jest otwarty, jeśli dla każdego punktu \( x \in U \) istnieje przedział otwarty \( (a, b) \) w \( \mathbb{R} \), taki że \( x \in (a, b) \) oraz \( (a, b) \cap (0,1) \subseteq U \).

Przedział \( (0,1) \) można więc zapisać jako przecięcie kilku zbiorów otwartych w \( \mathbb{R} \). Dzięki temu sam w sobie stanowi przestrzeń topologiczną z topologią indukowaną ze standardowej topologii na \( \mathbb{R} \).

Na przykład przedziały \( (0.1, 0.5) \), \( (0.2, 0.9) \) lub ich suma, jak \( (0.1, 0.5) \cup (0.6, 0.8) \), są zbiorami otwartymi w \( (0,1) \) w topologii indukowanej. Oznacza to, że zbiory otwarte w \( (0,1) \) to dokładnie te zbiory otwarte w \( \mathbb{R} \), których przecięcie z \( (0,1) \) pozostaje całkowicie zawarte w tym przedziale.

Ponieważ \( (0,1) \) jest podprzestrzenią topologiczną \( \mathbb{R} \), zachowuje wszystkie jej podstawowe własności.

Przykład 3

Rozważmy teraz skończony zbiór \( X = \{1,2,3\} \), złożony z trzech liczb naturalnych. Sprawdźmy, czy można wyposażyć go w strukturę topologiczną pochodzącą ze standardowej topologii na \( \mathbb{R} \).

W tym przypadku pojedyncze punkty nie mogą być zbiorami otwartymi, ponieważ baza topologii standardowej składa się z przedziałów otwartych, które zawsze zawierają nieskończenie wiele punktów. Dlatego taka