Spójność w topologii - jak przestrzeń trzyma się razem

W topologii mówimy, że przestrzeń jest spójna, jeśli nie da się jej rozdzielić na dwa rozłączne zbiory otwarte. W praktyce oznacza to, że w takiej przestrzeni można połączyć dowolne dwa punkty ciągłą ścieżką, nie wychodząc poza jej granice.

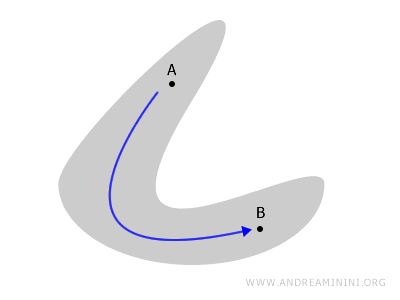
Spójność opisuje więc, jak różne części przestrzeni są ze sobą powiązane - albo przeciwnie, jak są od siebie oddzielone.

To jedno z kluczowych pojęć topologii, ściśle powiązane z ideą ciągłości.

Dzięki pojęciu spójności matematycy mogą lepiej zrozumieć strukturę przestrzeni i zależności między jej częściami. To właśnie ono pozwala klasyfikować i analizować różne typy przestrzeni topologicznych.

Przykład z życia - kiedy przestrzeń jest spójna?

Wyobraź sobie figurę płaską lub bryłę, w której każde dwa punkty A i B da się połączyć ciągłą ścieżką, nie wychodząc poza jej granice. Taka przestrzeń jest spójna.

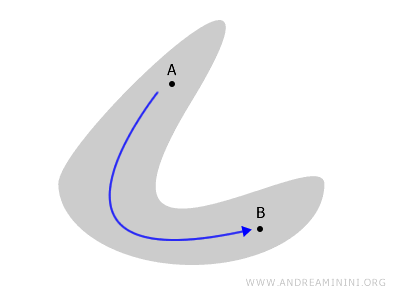
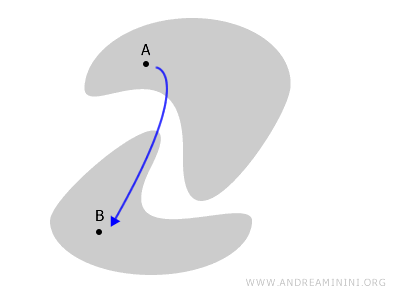
Jeśli jednak pewne części przestrzeni są od siebie oddzielone, nie da się ich połączyć w ten sposób. Wtedy mówimy, że przestrzeń jest niespójna.

Na przykład, gdy obszar dzieli się na dwie osobne części, każda ścieżka między punktami A i B musiałaby opuścić przestrzeń.

Dwa pokoje - prosty model niespójności

Aby to sobie wyobrazić, pomyśl o dwóch oddzielnych pokojach w tym samym budynku. Te pokoje odpowiadają dwóm rozłącznym zbiorom otwartym - nie obejmują ścian, które je rozdzielają, i nie mają wspólnych punktów.

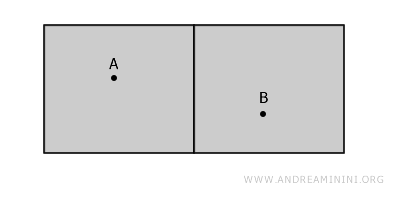
Choć pokoje są obok siebie, nie są połączone - bo każda droga z punktu A do punktu B musiałaby przejść przez ścianę, która nie należy do rozważanej przestrzeni.

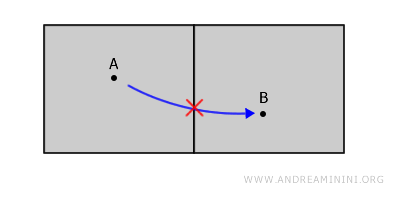
To pokazuje ważną zasadę: granice nie są częścią zbiorów otwartych.

Spójność lokalna - porządek wewnątrz chaosu

Spójność lokalna oznacza, że w pobliżu każdego punktu można znaleźć niewielki fragment przestrzeni, który sam w sobie jest spójny. Nawet jeśli cała przestrzeń jest niespójna, jej części mogą być lokalnie uporządkowane.

Wyobraź sobie znowu dwa pokoje - osobne, ale w każdym z nich panuje porządek i wewnętrzna spójność.

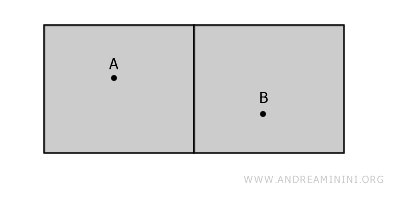
Przestrzeń jako całość jest niespójna, bo nie da się połączyć punktów A i B bez przekroczenia ściany. Ale punkt A znajduje się w spójnym otoczeniu - i to wystarczy, by mówić o spójności lokalnej.

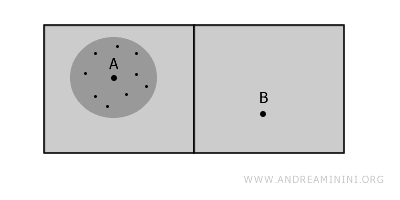
Analogicznie, punkt B ma własne, spójne otoczenie.

Rodzaje spójności

W topologii wyróżniamy kilka rodzajów spójności, ale dwie z nich są szczególnie ważne:

• Spójność topologiczna
  Przestrzeń topologiczną $ X $ nazywamy spójną, jeśli nie można jej przedstawić jako sumy dwóch rozłącznych, niepustych zbiorów otwartych. Innymi słowy, przestrzeni tej nie da się „rozciąć” na dwie niezależne części, które nie mają ze sobą żadnych punktów wspólnych.

  Przykład. Przedział (-1, 1) jest spójny, natomiast zbiór (-1, 0) ∪ (0, 1) już nie, ponieważ można go zapisać jako sumę dwóch rozłącznych i niepustych zbiorów otwartych - (-1, 0) oraz (0, 1) - które razem tworzą całą przestrzeń.
  Te dwa zbiory stanowią więc rozdzielenie przestrzeni.

• Spójność przez ścieżki (lub łukową)
  Przestrzeń topologiczną nazywamy spójną przez ścieżki, jeśli dla dowolnej pary punktów A i B istnieje ciągła ścieżka łącząca te punkty i w całości zawarta w danej przestrzeni. Każda przestrzeń spójna przez ścieżki jest również spójna w sensie topologicznym, choć nie zawsze zachodzi implikacja odwrotna.

  Na przykład, rozważmy zamkniętą figurę na płaszczyźnie. Dla dowolnych dwóch punktów wewnętrznych A i B można narysować ciągłą linię łączącą je bez odrywania ołówka od kartki i bez wychodzenia poza granice figury.
  
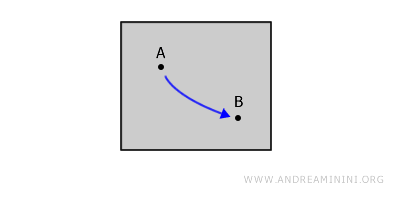
  Różnica między spójnością łukową a ścieżkową.  Spójność łukowa jest pojęciem zbliżonym do spójności przez ścieżki, lecz w tym przypadku ścieżka musi być iniektywna, czyli nie może się przecinać ani przechodzić więcej niż raz przez ten sam punkt.

• Spójność prosta
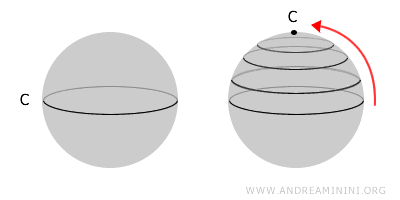
  Przestrzeń jest prosto spójna, jeśli każdą zamkniętą pętlę można „skurczyć" do punktu bez jej przerwania. Taka przestrzeń nie ma wewnętrznych dziur. Każda prosto spójna przestrzeń jest spójna, ale nie każda spójna jest prosto spójna.

  Na przykład sfera jest prosto spójna - każdą pętlę na jej powierzchni można stopniowo zmniejszać, aż zniknie w jednym punkcie. Torus (czyli „pączek" z otworem) jest natomiast spójny, lecz nie prosto spójny, bo jego otwór uniemożliwia takie przekształcenie.
  
  
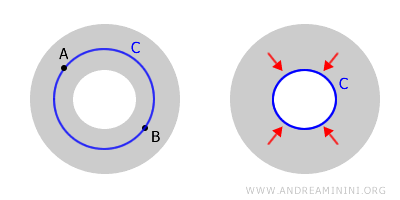
  Takie przestrzenie nazywamy wielokrotnie spójnymi. Klasycznym przykładem jest pierścień (czyli obszar w kształcie obrączki).

Na zakończenie

Warto zapamiętać jedno: wśród liczb rzeczywistych tylko przedziały są przestrzeniami spójnymi. To prosty, ale bardzo głęboki fakt, który dobrze oddaje istotę spójności - ciągłość bez przerw i pęknięć.