Spójność przestrzeni topologicznej

Definicja poprzez zbiory otwarte

Innymi słowy, przestrzeń jest spójna, gdy nie da się jej „rozciąć" na dwie oddzielne części otwarte, które w sumie dałyby całość. Gdy takie rozdzielenie jest możliwe, mówimy, że przestrzeń jest niespójna, a para $(U, V)$ tworzy rozcięcie przestrzeni $X$.

Uwaga. Jest to definicja spójności topologicznej oparta na zbiorach otwartych. W dalszej części zobaczymy, że nie zawsze pokrywa się ona z pojęciem „spójności ścieżkowej" lub „łukowej".

Przykład: trzy elementy, dwie topologie

Weźmy prosty zbiór trzech elementów:

$$ X = \{a, b, c\} $$

Możemy zdefiniować na nim dwa różne układy topologii:

• Topologia A
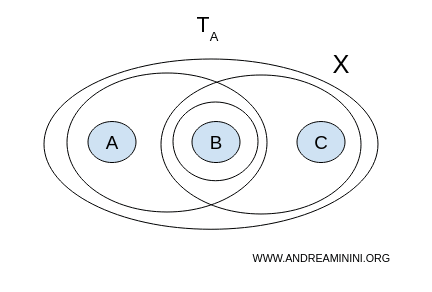
  $$ \mathcal{T}_A = \{ \emptyset, X, \{ a,b \}, \{ b \}, \{ b,c \} \} $$
• Topologia B
  $$ \mathcal{T}_B = \{ \emptyset, X, \{ a,b \}, \{ c \}, \{ b,c \} \} $$

Zadajmy więc pytanie: która z tych przestrzeni jest spójna?

🔹 Topologia A

Spróbujmy znaleźć rozcięcie $(U, V)$ w $ \mathcal{T}_A $. Szukamy dwóch niepustych, rozłącznych zbiorów otwartych, których suma dałaby całe $ X $.

• $ U = \{a,b\}, V = \{b,c\} $ - nie są rozłączne, bo oba zawierają $ b $;
• $ U = \{a,b\}, V = \{b\} $ - również nie;
• $ U = \{b\}, V = \{b,c\} $ - także nie.

Żadna kombinacja nie spełnia warunków rozcięcia. Oznacza to, że przy tej topologii przestrzeń $ X $ jest spójna.

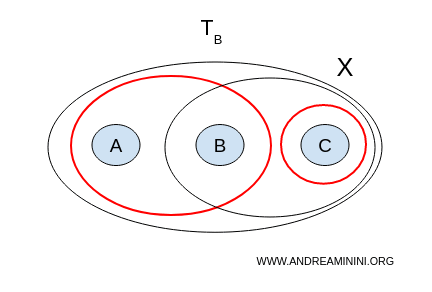
🔹 Topologia B

W przypadku topologii $ \mathcal{T}_B $ sytuacja wygląda inaczej.

• $ U = \{a,b\}, V = \{b,c\} $ - zbiory nakładają się w punkcie $ b $;
• $ U = \{a,b\}, V = \{c\} $ - są rozłączne, niepuste i razem dają całe $ X $.

Para $(U = \{a,b\}, V = \{c\})$ spełnia warunki rozcięcia, więc przestrzeń $ X $ z tą topologią jest niespójna.

Uwaga. Ten prosty przykład pokazuje, że spójność nie zależy wyłącznie od tego, jakie punkty tworzą przestrzeń, lecz także od przyjętej topologii. Dwie różne topologie mogą prowadzić do zupełnie odmiennych własności globalnych.

Przykład 2: prosta z usuniętym punktem

Rozważmy przestrzeń $ X $, w której $ n $ jest stałą liczbą rzeczywistą (np. $ n = 0 $):

$$ X = (-\infty, n) \cup (n, +\infty) $$

To po prostu prosta rzeczywista bez punktu $ n $:

$$ X = \mathbb{R} \setminus \{n\} $$

Sprawdźmy, czy ta przestrzeń jest spójna.

• $ U = (-\infty, n) $ i $ V = (n, +\infty) $ są otwarte w standardowej topologii na $ \mathbb{R} $;
• są rozłączne i niepuste;
• a ich suma to całe $ X $.

$$ U \neq \emptyset, \quad V \neq \emptyset, \quad U \cap V = \emptyset, \quad U \cup V = X $$

Spełnione są więc wszystkie warunki rozcięcia. Zatem przestrzeń $ X $ jest niespójna.

Uwaga. Usunięcie jednego punktu z prostej rzeczywistej „przerywa" jej ciągłość: linia dzieli się na dwie osobne części - po lewej i po prawej stronie $ n $. Nie można już przejść między nimi żadną ciągłą ścieżką. Dlatego przestrzeń ta jest zarówno niespójna topologicznie, jak i niespójna ścieżkowo.

Spójność a spójność ścieżkowa

Te dwa pojęcia często się mylą, ale oznaczają coś innego. Przestrzeń może być spójna topologicznie, choć nie będzie spójna ścieżkowo.

• Spójność topologiczna
  Przestrzeni nie da się rozdzielić na dwa rozłączne, niepuste zbiory otwarte.
• Spójność ścieżkowa
  Każde dwa punkty przestrzeni można połączyć ciągłą ścieżką całkowicie leżącą w tej przestrzeni. Jeśli ścieżka nie przecina żadnego punktu więcej niż raz, mówimy o spójności łukowej.

W skrócie: każda przestrzeń spójna ścieżkowo jest spójna, ale nie każda przestrzeń spójna musi być spójna ścieżkowo.

Ciągła ścieżka łącząca dwa punkty uniemożliwia „rozcięcie" przestrzeni na osobne części. Jednak odwrotnie - istnieją przestrzenie, które mimo że są spójne, nie da się w nich wyznaczyć takiej ścieżki.

Przykład. Klasyczny przykład to krzywa sinus topologa: $$ S = \{ (x, \sin(1/x)) \mid x > 0 \} \cup \{ (0, y) \mid -1 \le y \le 1 \} $$ Ta przestrzeń jest spójna, bo nie można jej rozdzielić na dwa rozłączne zbiory otwarte, lecz nie jest spójna ścieżkowo - nie istnieje ciągła ścieżka łącząca punkt na oscylującej krzywej z punktem na pionowym odcinku.

Uwagi

Dodatkowe spostrzeżenia dotyczące przestrzeni spójnych

• Twierdzenie: charakterystyka przestrzeni spójnych za pomocą zbiorów otwartych i domkniętych (clopen)
  Przestrzeń topologiczna \( X \) jest spójna wtedy i tylko wtedy, gdy jedynymi jej podzbiorami, które są jednocześnie otwarte i domknięte (clopen), są cała przestrzeń \( X \) oraz zbiór pusty \( \emptyset \).

I inne zagadnienia tego typu.