Przestrzenie łukowo spójne

Przestrzeń topologiczna S jest łukowo spójna, jeśli dla dowolnych dwóch punktów A i B można znaleźć ciągłą ścieżkę, która je łączy, nie wychodząc poza granice tej przestrzeni.

Wyobraź sobie zwykłą kartkę papieru - bez ramki, bez brzegów.

To idealny przykład obszaru ciągłego, otwartego, bez ograniczeń na krawędziach.

Na takiej kartce możesz połączyć dowolne dwa punkty A i B jednym, płynnym ruchem długopisu - bez odrywania go od powierzchni. To właśnie intuicyjny obraz łukowej spójności.

Inaczej mówiąc, każda możliwa ścieżka łącząca punkty A i B w całości mieści się w tej samej przestrzeni.

Każda przestrzeń łukowo spójna jest zarazem przestrzenią spójną.

Brzmi to naturalnie: jeśli przestrzeń nie jest „pocięta" na części, możemy przejść z jednego punktu do drugiego bez przeskakiwania poza jej granice.

Jednak uwaga - odwrotne twierdzenie nie działa. Nie każda przestrzeń spójna jest łukowo spójna.

Oto przykład, który świetnie to pokazuje - pozornie paradoksalny, ale w pełni poprawny matematycznie.

Weźmy dwa zbiory: Q i T.

$$ Q = \{ \forall \ x \ \in R-\{ 0 \} \ , \ \sin( \frac{1}{x} ) \} $$

$$ T = \{ \ 0 \} $$

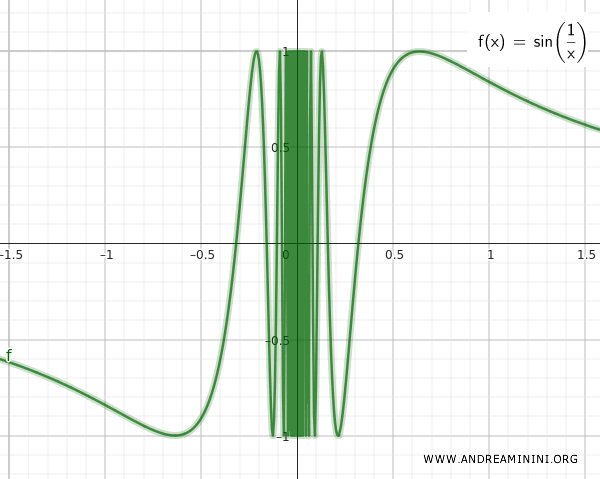
Zbiór Q zawiera punkty leżące na wykresie funkcji sin(1/x) dla wszystkich liczb rzeczywistych poza zerem. W punkcie x=0 funkcja nie jest określona, bo nie można dzielić przez zero.

Zbiór T składa się wyłącznie z punktu x=0.

Te dwa zbiory, Q i T, są nieskończenie bliskie sobie - na wykresie widać, że sinus coraz szybciej oscyluje wokół zera, zbliżając się do niego, ale nigdy go nie dotykając.

Teraz połączmy te dwa zbiory:

$$ S = Q \cup T $$

Zbiór S jest spójny. Dla każdego ε>0 znajdziemy w otoczeniu punktu 0 (czyli w przedziale (0-ε, 0+ε)) punkty należące do zbioru Q.

Dzieje się tak, ponieważ zero jest punktem skupienia funkcji sin(1/x) - wykres „gęsto" otacza tę wartość.

Mimo to zbiór S nie jest łukowo spójny. Nie da się narysować ciągłej ścieżki łączącej punkt z Q z punktem T, czyli z samym zerem, nie wychodząc poza zbiór S.

Uwaga: Gdybyśmy zamiast tego rozważyli funkcję f(x)=1/x, sytuacja wyglądałaby inaczej. Wtedy zbiory Q i T byłyby całkowicie rozłączne - nie zbliżałyby się do siebie w nieskończoność.

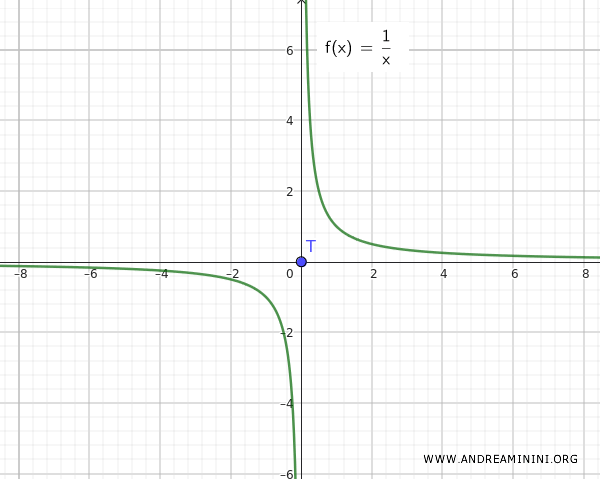
Ten przykład pokazuje, że połączenie zbioru spójnego Q={∀ x ∈ R-{0}, 1/x} z izolowanym punktem T={0} nie zawsze daje przestrzeń spójną - chyba że ten punkt (np. zero) jest jednocześnie punktem skupienia funkcji.

 Matematyka pełna jest takich subtelnych niuansów - i to właśnie one czynią topologię tak fascynującą.