Separacja podzbioru przez zbiory otwarte

Niech $ A $ będzie podzbiorem przestrzeni topologicznej $ X $. Aby dobrze zrozumieć, kiedy taki zbiór można uznać za rzeczywiście rozdzielony na dwie części, korzystamy z dwóch zbiorów otwartych $ U $ i $ V $. Mówimy, że tworzą one separację zbioru $ A $, jeśli spełniają trzy przejrzyste warunki:

wspólnie pokrywają cały zbiór \[ A \subseteq U \cup V \]
każdy z nich zawiera przynajmniej jeden punkt $ A $ \[ U \cap A \neq \varnothing \] \[ V \cap A \neq \varnothing \]
żaden punkt $ A $ nie leży jednocześnie w $ U $ i $ V $ \[ U \cap V \cap A = \varnothing \]

Te trzy warunki tworzą podstawowy schemat, który pozwala stwierdzić, czy podzbiór jest faktycznie rozdzielony na dwie części. Jedna z nich znajduje się w całości w $ U $, druga w $ V $, a między nimi nie ma żadnego punktu wspólnego. To właśnie ta rozłączność względem $ A $ sprawia, że możemy mówić o separacji w sensie topologicznym.

Tego typu podejście jest często stosowane w topologii ogólnej. Pozwala przełożyć intuicję o „dwóch osobnych fragmentach zbioru" na ścisły język matematyczny oparty na zbiorach otwartych.

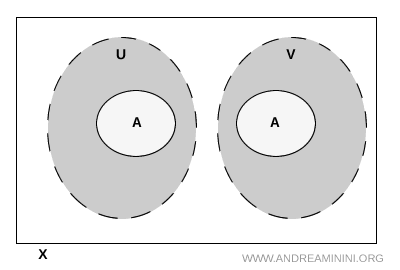
schemat separacji podzbioru A za pomocą dwóch zbiorów otwartych U i V

Uwaga. Zbiory $ U $ i $ V $ mogą przecinać się poza obszarem $ A $. Nie wpływa to na separację, o ile przecięcie nie zawiera punktów należących do $ A $. Ważne jest wyłącznie to, co dzieje się w obrębie badanego podzbioru.
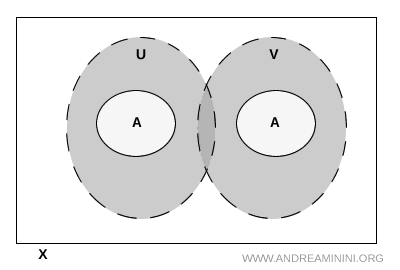
schemat podkreślający, że przecięcie U i V poza A nie wpływa na separację

Przykład

Przyjrzyjmy się temu na konkretnym przykładzie w przestrzeni $ X = \mathbb{R} $. Weźmy zbiór:

$$ A = [-2,-1] \cup [1,2] $$

To dwa wyraźnie oddzielone przedziały domknięte. Idealna sytuacja, by zobaczyć, jak działa separacja.

Wybierzmy otwarte przedziały:

$$ U = (-3,0) $$

$$ V = (0,3) $$

Na osi liczbowej wygląda to następująco:

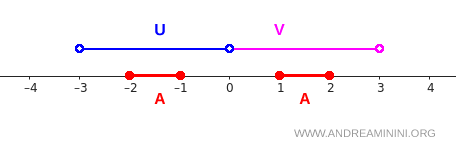
oś R z przedziałami U i V oraz zbiorem A

Przedział $ [-2,-1] $ leży w całości w $ U $, a $ [1,2] $ w $ V $. Sprawdźmy teraz warunki separacji krok po kroku.

1. Cały zbiór $ A $ należy do sumy $ U $ i $ V $:

$$ A \subseteq U \cup V $$

2. Każdy z otwartych przedziałów faktycznie „dotyka" $ A $:

$$ U \cap A = [-2,-1] \neq \varnothing $$

$$ V \cap A = [1,2] \neq \varnothing $$

3. Nie ma punktu, który należałby do $ U $, $ V $ i $ A $ jednocześnie:

$$ U \cap V \cap A = \varnothing $$

Wszystkie trzy warunki są spełnione, więc $ U $ i $ V $ rzeczywiście separują zbiór $ A $. W tym przykładzie widać to wyjątkowo wyraźnie: mamy dwa fragmenty zbioru oddalone od siebie, a odpowiednio dobrane zbiory otwarte przechwytują je osobno. To dokładnie ten układ, który pozwala najlepiej zrozumieć ogólną definicję separacji.