Suma wnętrz dwóch zbiorów
Suma wnętrz zbiorów \( A \) i \( B \) jest zawsze podzbiorem wnętrza ich sumy: \[ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) \] Choć relacja ta jest ogólna, równość zachodzi jedynie w szczególnych sytuacjach.
Wnętrze sumy to obszar, w którym każdy punkt ma w pełni zawarte w tym zbiorze otoczenie. Natomiast suma wnętrz uwzględnia tylko te punkty, które już należą do wnętrz poszczególnych zbiorów. Różnica między tymi konstrukcjami okazuje się bardzo istotna w analizie topologicznej, szczególnie wtedy, gdy zbiory stykają się na granicach lub częściowo się pokrywają.
Przykład 1: przedziały otwarte
Rozważmy dwa otwarte przedziały na prostej rzeczywistej:
$$ A = (0, 2) \qquad B = (1, 3) $$
Wnętrza tych przedziałów są równe im samym, dlatego:
$$ \text{Int}(A) = (0, 2), \qquad \text{Int}(B) = (1, 3) $$
Suma wnętrz daje przedział:
$$ (0, 2) \cup (1, 3) = (0, 3) $$
Natomiast suma zbiorów \( A \cup B \) również tworzy przedział otwarty \( (0, 3) \), którego wnętrze jest takie samo. W tym przypadku oba zbiory idealnie się uzupełniają, dlatego równość zachodzi:
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
Przykład 2: przedziały domknięte
Teraz spójrzmy na dwa przedziały domknięte:
$$ A = [0, 2] \qquad B = [2, 3] $$
Wnętrza tych zbiorów to odpowiednio \( (0, 2) \) oraz \( (2, 3) \). Ich suma:
$$ A \cup B = [0, 3] $$
ma wnętrze:
$$ \text{Int}(A \cup B) = (0, 3) $$
Choć inkluzja pozostaje prawdziwa:
$$ (0, 2) \cup (2, 3) \subseteq (0, 3), $$
punkt \( 2 \) stanowi wyraźny dowód, że równość już nie zachodzi. Należy on do wnętrza sumy, ale nie znajduje się w żadnym wnętrzu indywidualnym. To klasyczny przykład, który pokazuje, że granice zbiorów mogą decydować o ścisłości inkluzji.
Przykład 3: dyski w przestrzeni \(\mathbb{R}^2\)
Przenieśmy się teraz na płaszczyznę. Zbiory \( A \) i \( B \) to dwa otwarte dyski o promieniu 1, których środki leżą w punktach \( (0, 0) \) oraz \( (0{,}5, 0) \). Ze względu na częściowe nakładanie się dysków ich suma tworzy ciągły region zawierający obszar wspólny.
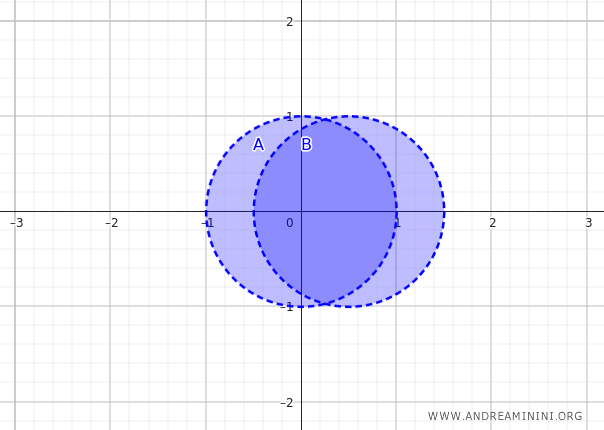
Ponieważ oba dyski są otwarte, ich wnętrza pokrywają się z nimi w całości. Wnętrze ich sumy jest również równe sumie dysków. Znów zachodzi relacja:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
Dlaczego ta własność zawsze działa?
Klucz tkwi w samej definicji wnętrza. Jeśli punkt należy do wnętrza \( A \) lub \( B \), to istnieje wokół niego otwarte otoczenie w całości zawarte w danym zbiorze. A ponieważ każdy z tych zbiorów jest podzbiorem sumy, to to samo otoczenie znajduje się również w \( A \cup B \).
Z tego powodu każdy punkt sumy wnętrz musi należeć do wnętrza sumy. Otrzymujemy więc uniwersalną, zawsze prawdziwą inkluzję:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B). $$
Jednak dopiero analiza szczegółowych przykładów pozwala zrozumieć, kiedy inkluzja ta staje się równością, a kiedy pozostaje ścisła. Granice, punkty styku i sposób, w jaki zbiory zachodzą na siebie, odgrywają tu zasadniczą rolę.