Charakterystyka brzegu zbioru

Punkt $ x $ należy do brzegu zbioru $ A $, jeżeli w każdym jego otoczeniu znajdują się jednocześnie punkty należące do zbioru $ A $ oraz punkty należące do jego dopełnienia $ X - A $.

Mówiąc inaczej, jeżeli nie da się znaleźć żadnego otoczenia punktu $ x $, które byłoby w całości zawarte wyłącznie w $ A $ lub wyłącznie w $ X - A $, to punkt $ x $ jest punktem brzegowym zbioru $ A $.

Przykład ilustrujący pojęcie brzegu
Uzasadnienie

Przykład ilustrujący pojęcie brzegu

Aby lepiej zrozumieć tę definicję, rozważmy prosty i intuicyjny przykład.

Niech $ A = (0, 1) $ będzie przedziałem otwartym na prostej rzeczywistej $ \mathbb{R} $.

Punkty 0 oraz 1 należą do brzegu zbioru $ A $, ponieważ każde ich otoczenie zawiera zarówno punkty leżące wewnątrz przedziału $ (0, 1) $, jak i punkty położone poza nim.

Punkt 1
Każde otoczenie postaci $ (1 - \epsilon, 1 + \epsilon) $, dla dowolnie małego ε, zawiera fragment $ (1 - \epsilon, 1) $ należący do zbioru $ A $ oraz fragment $ (1, 1 + \epsilon) $ leżący w jego dopełnieniu. Oznacza to, że punkt 1 jest punktem brzegowym zbioru $ A $.
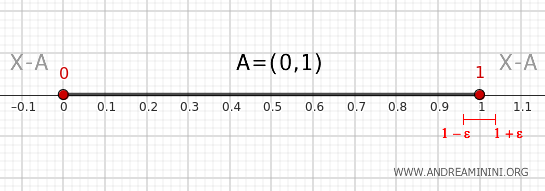
Punkt 0
W analogiczny sposób każde otoczenie $ (0 - \epsilon, 0 + \epsilon) $ zawiera część $ (0, 0 + \epsilon) $ należącą do zbioru $ A $ oraz część $ (0 - \epsilon, 0) $ należącą do jego dopełnienia. Zatem punkt 0 również jest punktem brzegowym zbioru $ A $.
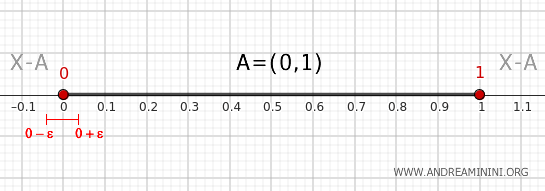
Punkt wewnętrzny przedziału (0, 1)
Każdy punkt $ x $ leżący ściśle między 0 a 1 posiada takie otoczenie $ (x - \epsilon, x + \epsilon) $, gdzie ε > 0, które w całości zawiera się w zbiorze $ A $. Otoczenie to nie przecina dopełnienia, dlatego punkty te nie należą do brzegu zbioru.
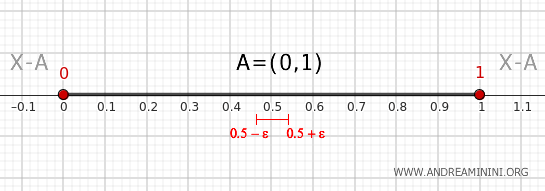
Punkt zewnętrzny względem przedziału (0, 1)
Każdy punkt leżący ściśle poza przedziałem $ (0, 1) $, z wyjątkiem punktów 0 i 1, ma otoczenie $ (x - \epsilon, x + \epsilon) $ w całości zawarte w zbiorze $ X - A $, bez punktów wspólnych ze zbiorem $ A $. Punkty te nie są więc punktami brzegowymi.

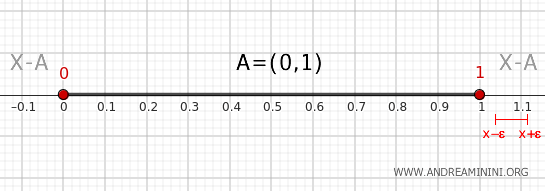
Z powyższej analizy wynika, że jedynymi punktami brzegowymi zbioru $ A $ są punkty 0 oraz 1:

$$ \partial A = \{0,1\} $$

Podsumowując, punkt $ x $ należy do brzegu zbioru $ A $ wtedy i tylko wtedy, gdy nie istnieje żadne jego otoczenie, które byłoby w całości zawarte ani w $ A $, ani w jego dopełnieniu. Kryterium to pozwala w prosty i jednoznaczny sposób rozpoznać punkty brzegowe.

Uzasadnienie

Aby formalnie uzasadnić tę charakterystykę, rozważmy dwie implikacje :

1] Załóżmy, że $ x \in \partial A $

Z definicji brzegu zbioru wynika, że:

$$ x \in \text{Cl}(A) \quad \text{i} \quad x \notin \text{Int}(A) $$

Warunek $ x \in \text{Cl}(A) $ oznacza, że każde otoczenie punktu $ x $ ma część wspólną ze zbiorem $ A $.

Natomiast fakt, że $ x \notin \text{Int}(A) $, oznacza, iż żadne otoczenie punktu $ x $ nie jest w całości zawarte w $ A $, a więc każde z nich zawiera również punkty należące do zbioru $ X - A $.

W konsekwencji każde otoczenie punktu $ x $ przecina jednocześnie zbiór $ A $ oraz jego dopełnienie.

2] Załóżmy, że każde otoczenie punktu $ x $ przecina zarówno $ A $, jak i $ X - A $

Wówczas, zgodnie z definicją domknięcia, mamy $ x \in \text{Cl}(A) $ oraz $ x \in \text{Cl}(X - A) $.

Ponieważ zachodzi równość $ \text{Cl}(X - A) = X - \text{Int}(A) $, otrzymujemy stąd, że $ x \notin \text{Int}(A) $.

Ostatecznie dostajemy:

$$ x \in \text{Cl}(A) \setminus \text{Int}(A) = \partial A $$

Dowodzi to, że implikacja odwrotna również zachodzi, a punkt $ x $ jest rzeczywiście punktem brzegowym zbioru $ A $.