Verzamelingen die niet open en niet gesloten zijn

In de topologie noemt men een verzameling noch open noch gesloten wanneer zij niet voldoet aan de eigenschappen die nodig zijn om tot een van beide categorieën te behoren.

Dit doet zich voor in topologische ruimten waarin een verzameling niet kan worden aangemerkt als een open verzameling en ook niet als het complement van een open verzameling. In dat geval valt zij buiten beide standaardclassificaties.

Zo’n verzameling kan dus ook niet worden beschouwd als een gesloten verzameling.

Opmerking: In de standaardtopologie op de reële getallen is het soms lastig voor te stellen dat er verzamelingen bestaan die noch open noch gesloten zijn. In meer algemene topologische ruimten komt dit echter regelmatig voor. Een concreet voorbeeld maakt het begrip direct duidelijk.

Concreet voorbeeld

Beschouw de verzameling \( X = \{a,b,c,d\} \) met een topologie \( T \) die bestaat uit de volgende open verzamelingen: \( \{b\} \), \( \{a,b\} \), \( \{c,d\} \), \( \{b,c,d\} \), \( \{a,b,c,d\} \) en de lege verzameling (Ø). Deze selectie bepaalt welke deelverzamelingen in deze topologie als open worden beschouwd.

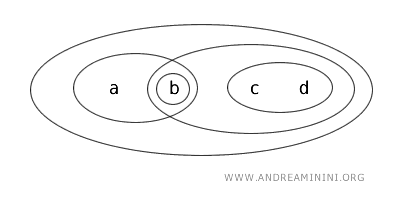
We richten ons nu op de deelverzameling \( \{b,c\} \) van \( X \).

• De verzameling \( \{b,c\} \) is niet open in \( T \), want zij komt niet voor in de lijst met open verzamelingen.
• Daarnaast is \( \{b,c\} \) ook niet gesloten, omdat haar complement \( X \setminus \{b,c\} = \{a,d\} \) geen open verzameling is in \( T \).

Daarom is de verzameling \( \{b,c\} \) in de topologie \( T \) noch open noch gesloten.

Dit voorbeeld laat zien dat de klassieke intuïtie uit de reële getallen niet altijd opgaat. In meer algemene topologische ruimten kunnen verzamelingen eigenschappen hebben die afwijken van de bekende gevallen, wat de topologie juist tot een veelzijdig en krachtig vakgebied maakt.