Fórmula del Coseno de la Diferencia
La fórmula que permite calcular el coseno de la diferencia entre dos ángulos es: $$ \cos(\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta $$
Por tanto, nunca es correcto escribir:
$$ \cos (\alpha - \beta) = \cos \alpha - \cos \beta $$
Ejemplo práctico
Sabemos que el coseno de 90° (π/2) es 0 y que el de 60° (π/3) es 1/2:
$$ \cos \frac{\pi}{2} = 0 $$
$$ \cos \frac{\pi}{3} = \frac{1}{2} $$
Queremos calcular el coseno de la diferencia entre estos dos ángulos:
$$ \cos \left( \frac{\pi}{2} - \frac{\pi}{3} \right) $$
Aplicando la fórmula del coseno de la diferencia con α = π/2 y β = π/3:
$$ \cos \left( \frac{\pi}{2} - \frac{\pi}{3} \right) = \cos \frac{\pi}{2} \cos \frac{\pi}{3} + \sin \frac{\pi}{2} \sin \frac{\pi}{3} $$
$$ = 0 \cdot \frac{1}{2} + 1 \cdot \frac{\sqrt{3}}{2} = \frac{\sqrt{3}}{2} $$
Nota: Obsérvese que $$ \cos \left( \frac{\pi}{2} - \frac{\pi}{3} \right) \ne \cos \left( \frac{\pi}{2} \right) - \cos \left( \frac{\pi}{3} \right) = 0 - \frac{1}{2} $$
Verificación
$$ \cos \left( \frac{\pi}{2} - \frac{\pi}{3} \right) = \cos \left( \frac{3\pi - 2\pi}{6} \right) = \cos \left( \frac{\pi}{6} \right) = \frac{ \sqrt{3} }{2} $$
Demostración
Dibujamos los ángulos α y β sobre una circunferencia unitaria, con α > β.
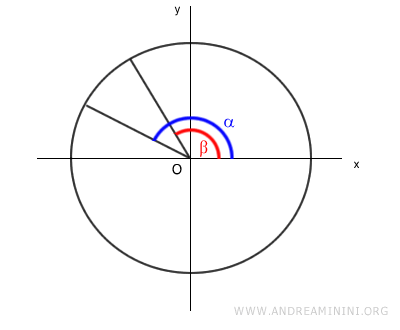
La diferencia α - β define el ángulo que se muestra a continuación:
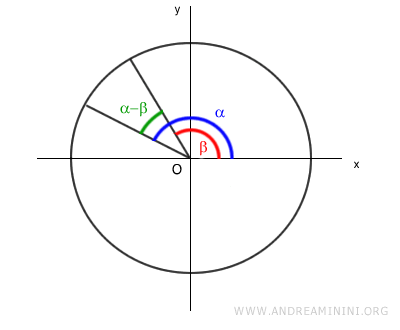
Consideramos ahora el mismo ángulo, pero medido desde el eje horizontal:
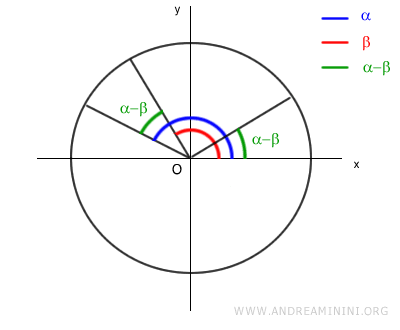
Los triángulos OAB y OCD son congruentes, ya que tienen los mismos ángulos y lados correspondientes:
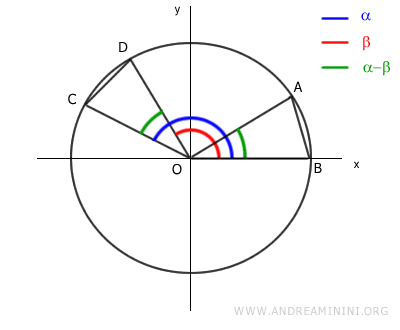
Por lo tanto, los segmentos AB y CD tienen la misma longitud:
$$ \overline{AB} = \overline{CD} $$
Esto implica que:
$$ \overline{AB}^2 = (x_A - x_B)^2 + (y_A - y_B)^2 $$
$$ \overline{CD}^2 = (x_C - x_D)^2 + (y_C - y_D)^2 $$
Como ambas distancias son iguales, podemos escribir:
$$ (x_A - x_B)^2 + (y_A - y_B)^2 = (x_C - x_D)^2 + (y_C - y_D)^2 $$
Sustituimos las coordenadas por sus expresiones trigonométricas:
Sabemos que \( x_A = \cos(\alpha - \beta) \) y \( y_A = \sin(\alpha - \beta) \):
$$ (\cos(\alpha - \beta) - x_B)^2 + (\sin(\alpha - \beta) - y_B)^2 = (x_C - x_D)^2 + (y_C - y_D)^2 $$
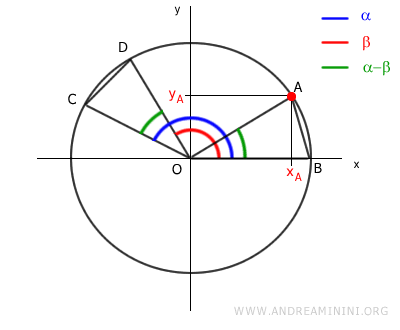
Y como \( x_B = \cos(0) = 1 \) y \( y_B = \sin(0) = 0 \):
$$ (\cos(\alpha - \beta) - 1)^2 + (\sin(\alpha - \beta))^2 = (x_C - x_D)^2 + (y_C - y_D)^2 $$
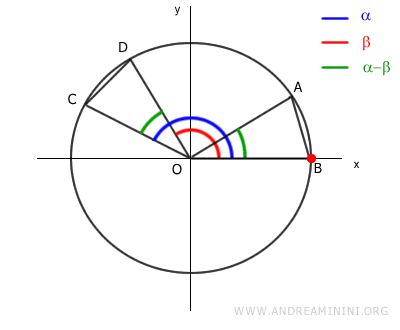
Además, \( x_C = \cos(\alpha) \) y \( y_C = \sin(\alpha) \):
$$ (\cos(\alpha - \beta) - 1)^2 + (\sin(\alpha - \beta))^2 = (\cos \alpha - x_D)^2 + (\sin \alpha - y_D)^2 $$
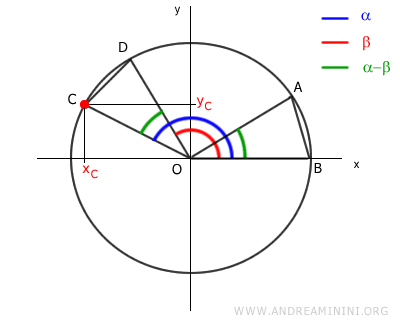
Y \( x_D = \cos(\beta) \), \( y_D = \sin(\beta) \), por lo que:
$$ (\cos(\alpha - \beta) - 1)^2 + (\sin(\alpha - \beta))^2 = (\cos \alpha - \cos \beta)^2 + (\sin \alpha - \sin \beta)^2 $$
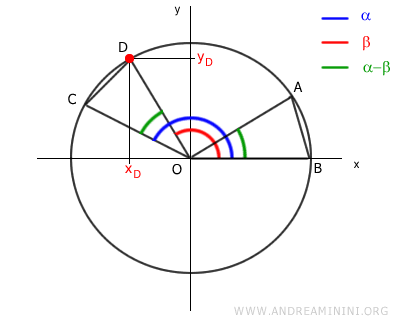
Desarrollamos ambos lados:
$$ \cos^2(\alpha - \beta) - 2 \cos(\alpha - \beta) + 1 + \sin^2(\alpha - \beta) = \\ = \cos^2 \alpha - 2 \cos \alpha \cos \beta + \cos^2 \beta + \sin^2 \alpha - 2 \sin \alpha \sin \beta + \sin^2 \beta $$
Aplicando la identidad pitagórica: $$ \cos^2(\theta) + \sin^2(\theta) = 1 $$ para cualquier ángulo \( \theta \), obtenemos:
$$ 1 - 2 \cos(\alpha - \beta) + 1 = 1 - 2 \cos \alpha \cos \beta - 2 \sin \alpha \sin \beta + 1 $$
Entonces:
$$ 2 - 2 \cos(\alpha - \beta) = 2 - 2 \cos \alpha \cos \beta - 2 \sin \alpha \sin \beta $$
Restando 2 en ambos lados:
$$ -2 \cos(\alpha - \beta) = -2 \cos \alpha \cos \beta - 2 \sin \alpha \sin \beta $$
Multiplicamos por -1:
$$ 2 \cos(\alpha - \beta) = 2 \cos \alpha \cos \beta + 2 \sin \alpha \sin \beta $$
Y dividiendo entre 2:
$$ \cos(\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta $$
Demostración completada.